本文作者:p0n1@安比实验室
libsnark 是目前实现 zk-SNARKs 电路最重要的框架,在众多私密交易或隐私计算相关项目间广泛应用,其中最著名当然要数 Zcash。Zcash 在 Sapling 版本升级前一直使用 libsnark 来实现电路(之后才替换为 bellman)。毫不夸张地说,libsnark 支撑并促进了 zk-SNARKs 技术的首次大规模应用,填补了零知识证明技术从最新理论到工程实现间的空缺。
希望通过本系列文章,所有开发者都能亲自上手实践,在短时间内迅速入门 libsnark,一步步了解 libsnark 的基本概念,学会如何开发 zk-SNARKs 电路,完成证明的生成和验证,最终将零知识证明应用到真实业务中去。
1. zk-SNARKs 和 libsnark 背景简介
零知识证明,可能是目前最具应用前景和想象力的密码学黑科技。而 zk-SNARKs 正是一类零知识证明方案的简称,全称为 Zero-Knowledge Succinct Non-interactive Arguments of Knowledge。这一名字几乎包含了其所有技术特征,即可以在不泄露任何其他信息的前提下证明一个命题的正确性,并且最终生成的证明具有简洁性(Succinct),也就是说最终生成的证明足够小,并且与计算量大小无关,是一个常数。用白话说就是,你理论上可以在不暴露任何隐私的情况下向其他所有人证明某件事,并且生成的证明体积很小,校验成本很低,与需要证明的内容计算量无关。听起来简直太美好了!
zk-SNARKs 能应用到很多场景,比如隐私保护、区块链扩容、可验证计算等。本文不介绍 zk-SNARKS 和零知识证明的理论细节,不熟悉或想深入了解的同学可阅读其他文章或论文。
如 Vitalik 写的关于 zk-SNARKs 著名的三篇博文。
https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627
https://medium.com/@VitalikButerin/zk-snarks-under-the-hood-b33151a013f6
或者阅读向程@HUST写的「深入浅出零知识证明之zk-SNARKs」,还有东泽写的「浅谈零知识证明之二:简短无交互证明(SNARK)」。
当然也欢迎关注安比实验室「探索零知识证明」系列和「从零开始学习 zk-SNARK」系列,以及从安比实验室维护的「零知识证明学习资源汇总」中查找更多资料。
本文主角 libsnark 是用于开发 zk-SNARKs 应用的 C++ 代码库,由 SCIPR Lab 开发并维护。libsnark 工程实现背后的理论基础是近年来(尤其是 2013 年以来)零知识证明特别是 zk-SNARKs 方向的一系列重要论文。如以下最著名的数篇:
[GGPR13] Quadratic span programs and succinct NIZKs without PCPs , Rosario Gennaro, Craig Gentry, Bryan Parno, Mariana Raykova, EUROCRYPT 2013
[PGHR13] Pinocchio: Nearly Practical Verifiable Computation , Bryan Parno, Craig Gentry, Jon Howell, Mariana Raykova, IEEE Symposium on Security and Privacy (Oakland) 2013
[BCGTV13] SNARKs for C: Verifying Program Executions Succinctly and in Zero Knowledge , Eli Ben-Sasson, Alessandro Chiesa, Daniel Genkin, Eran Tromer, Madars Virza, CRYPTO 2013
[BCIOP13] Succinct non-interactive arguments via linear interactive Proofs , Nir Bitansky, Alessandro Chiesa, Yuval Ishai, Rafail Ostrovsky, Omer Paneth, Theory of Cryptography Conference 2013
[BCTV14a] Succinct non-interactive zero knowledge for a von Neumann architecture , Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, Madars Virza, USENIX Security 2014
[BCTV14b] Scalable succinct non-interactive arguments via cycles of elliptic curves , Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, Madars Virza, CRYPTO 2014
[Groth16] On the Size of Pairing-based Non-interactive Arguments , Jens Groth, EUROCRYPT 2016
libsnark 的开发者们亦是这个领域内顶尖的学者或研究牛人,如 Eran Tromer 更是以上多篇论文的共同作者。
扎实的理论基础和工程能力,让 libsnark 的作者们能够化繁为简,将形如下图的高深理论和复杂公式逐一实现,高度工程化地抽象出简洁的接口供广大开发者方便地调用。向这些将非凡的理论研究推广至更大规模应用的先锋们致敬。

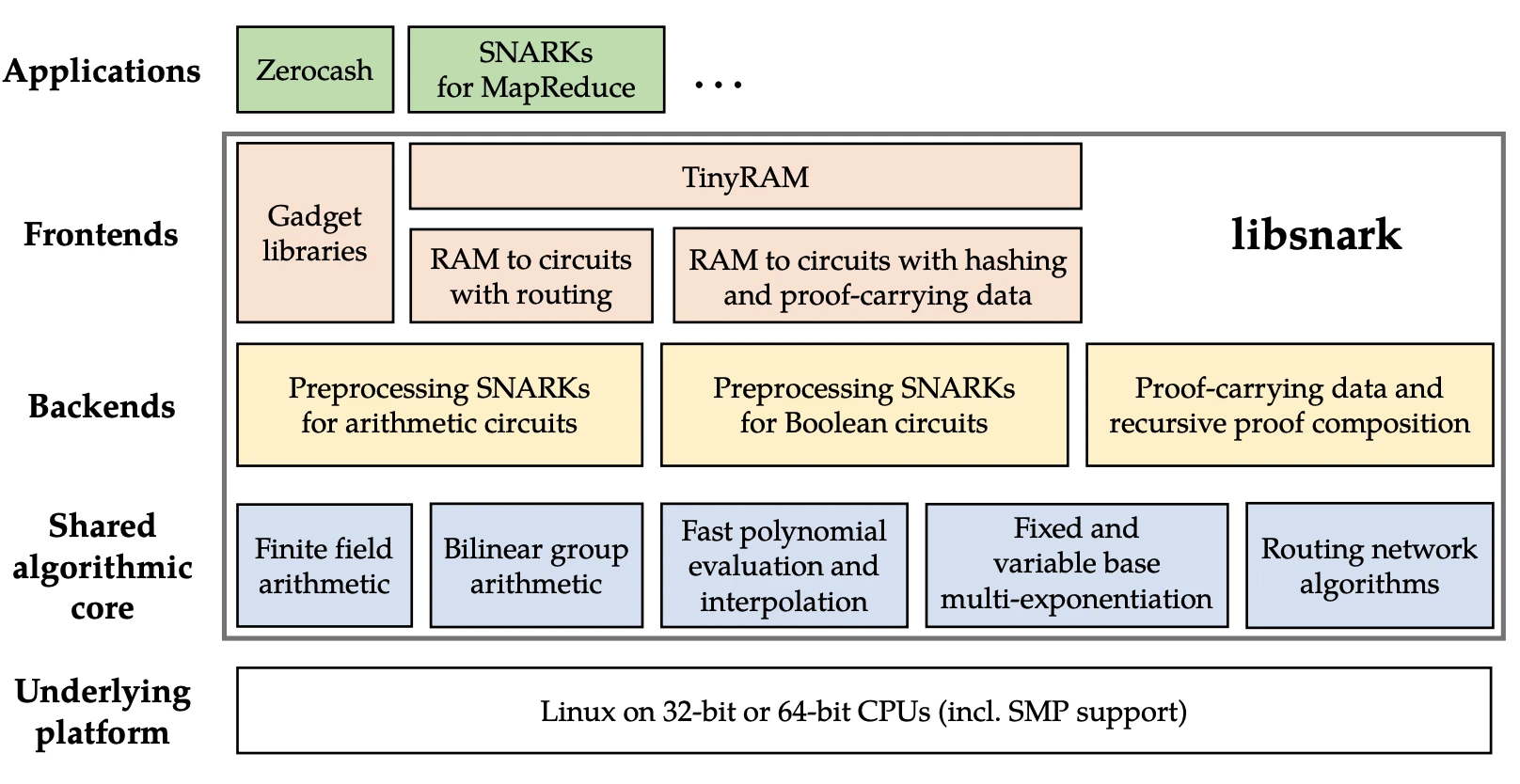
下图是 libsnark 的模块总览图,摘自 libsnark 代码贡献量第一作者 Madars Virza 在 MIT 的博士论文。
)
libsnark 框架提供了多个通用证明系统的实现,其中使用较多的是 BCTV14a 和 Groth16。
查看 libsnark/libsnark/zk_proof_systems 路径,就能发现 libsnark 对各种证明系统的具体实现,并且均按不同类别进行了分类,还附上了实现依照的具体论文。
其中:
zk_proof_systems/ppzksnark/r1cs_ppzksnark 对应的是 BCTV14a
zk_proof_systems/ppzksnark/r1cs_gg_ppzksnark 对应的是 Groth16
如果想研究这两个协议的实现细节可直接从这两个目录入手。ppzksnark 是指 preprocessing zkSNARK。这里的 pp/preprocessing 其实就是指我们常说的 trusted setup,即在证明生成和验证之前,需要通过一个生成算法来创建相关的公共参数(proving key 和 verification key)。我们也把这个提前生成的参数称为 「公共参考串」(Common Reference String),或简称为 CRS。
2. 基本原理与步骤
利用 libsnark 库开发 zk-SNARKs 应用从原理上可简要概括为以下四个步骤:
将待证明的命题表达为 R1CS (Rank One Constraint System)
使用生成算法(G)为该命题生成公共参数
使用证明算法(P)生成 R1CS 可满足性的证明
使用验证算法(V)来验证证明
不妨用一个十分简短(简化)的例子,来对照上面四个步骤。该例子模仿自这篇文章。
有这样一个函数 C(x, out),用于判断秘密 x 是否满足等式 x^3 + x + 5 == out,若满足则返回 true。
function C(x, out) {
return ( x^3 + x + 5 == out );
}
第一步,我们需要将函数 C(x, out) 在 libsnark 中进行表达。此处先省略,后面介绍详细过程。
第二步,对应下面的 Generator 函数(G),lambda 为随机产生,也就是常说的 trusted setup 过程中产生的 toxic waste。人们喜欢称它为“有毒废物”,是因为它必须被妥善处理(如必须销毁,不能让任何人知道),否则会影响证明协议安全。
lambda <- random()
(pk, vk) = G(C, lambda)
最终生成 proving key (pk) 和 verification key (vk)。
第三步,对应使用 Prove 函数(P)生成证明。这里想证明的是 prover 知道一个秘密值 x 和计算结果 out 可使等式满足。因此将 x、out 还有 pk 作为输入一起传给 P,最终生成证明 proof。
proof = P(pk, out, x)
第四步,对应使用 Verify 函数(V)验证证明,将 proof、out 还有 vk 传给 G,即可在不暴露秘密的情况下证明存在一个秘密值可使等式满足。
V(vk, out, proof) ?= true
而开发者主要工作量就集中在第一步,需要按照 libsnark 的接口规则手写 C++ 电路代码来描述命题,由代码构造 R1CS 约束。整个过程也即对应下图的 Computation -> Arithmetic Circuit -> R1CS。

3. 搭建 zk-SNARKs 应用开发环境
下面进入动手环节,快速上手 libsnark,跑通例子。
先下载本文对应的 libsnark 最小可用例子代码库 libsnark_abc。
git clone https://github.com/sec-bit/libsnark_abc.git
通过 git submodule 拉取 libsnark 代码。
cd libsnark_abc
git submodule update --init --recursive
参考 libsnark 项目文档完成相关依赖安装。以 Ubuntu 16.04 LTS 为例,需安装以下组件:
sudo apt-get install build-essential cmake git libgmp3-dev libprocps4-dev python-markdown libboost-all-dev libssl-dev
初始化 build 文件夹。
mkdir build cd build cmake ..
这步在 macOS 系统可能会遇到问题,参考这个 issue 处理。或尝试使用以下命令:
mkdir build cd build CPPFLAGS=-I/usr/local/opt/openssl/include LDFLAGS=-L/usr/local/opt/openssl/lib PKG_CONFIG_PATH=/usr/local/opt/openssl/lib/pkgconfig cmake -DWITH_PROCPS=OFF -DWITH_SUPERCOP=OFF ..
成功后,依旧在 build 目录进行编译。
make
编译成功后,在 build/src 目录中可看到 3 个二进制文件。
main
range
test
到这儿,你就以及完成示例项目的编译啦。尝试运行示例代码吧。
./src/main
最终出现如下日志,则说明一切正常。你已顺利拥有了 zkSNARK 应用开发环境,并成功跑了第一个 zk-SNARKs 的 demo。
4. 理解示例代码
下面我们一起来仔细瞅瞅代码。示例项目包含了 3 份代码(也可查看文末附录)。
不妨先看看 src/main.cpp。这个例子来自 Howard Wu 的 libsnark_tutorial,他也是 libsnark 作者之一哦。本文 libsnark_abc 的项目结构就是依照他的 libsnark_tutorial 搭建,属于“官方推荐风格” ,请放心食用 😆。
只有区区几十行代码,其中 run_r1cs_gg_ppzksnark() 是主要部分。很容易发现,真正起作用的实质代码只有下面 5 行。
r1cs_gg_ppzksnark_keypair<ppT> keypair = r1cs_gg_ppzksnark_generator<ppT>(example.constraint_system);
r1cs_gg_ppzksnark_processed_verification_key<ppT> pvk = r1cs_gg_ppzksnark_verifier_process_vk<ppT>(keypair.vk);
r1cs_gg_ppzksnark_proof<ppT> proof = r1cs_gg_ppzksnark_prover<ppT>(keypair.pk, example.primary_input, example.auxiliary_input);
const bool ans = r1cs_gg_ppzksnark_verifier_strong_IC<ppT>(keypair.vk, example.primary_input, proof);
const bool ans2 = r1cs_gg_ppzksnark_online_verifier_strong_IC<ppT>(pvk, example.primary_input, proof);
仅从“超长”的函数名就能看出来每步是在做什么,但是却看不到如何构造电路的细节。实际上这里仅仅是调用了自带的 r1cs_example,隐去了实现细节。
既然如此,那让我们通过一个更直观的例子来学习电路细节。研究 src/test.cpp,这个例子改编自 Christian Lundkvist 的 libsnark-tutorial。
代码开头仅引用了三个头文件,分别是:
#include <libsnark/common/default_types/r1cs_gg_ppzksnark_pp.hpp>
#include <libsnark/zk_proof_systems/ppzksnark/r1cs_gg_ppzksnark/r1cs_gg_ppzksnark.hpp>
#include <libsnark/gadgetlib1/pb_variable.hpp>
前面提到 r1cs_gg_ppzksnark 对应的是 Groth16 方案。这里加了 gg 是为了区别 r1cs_ppzksnark(也就是 BCTV14a 方案),表示 Generic Group Model(通用群模型)。Groth16 安全性证明依赖 Generic Group Model,以更强的安全假设换得了更好的性能和更短的证明。
第一个头文件是为了引入 default_r1cs_gg_ppzksnark_pp 类型,第二个则为了引入证明相关的各个接口。pb_variable 则是用来定义电路相关的变量。
下面需要进行一些初始化,定义使用的有限域,并初始化曲线参数。这是相当于每次的准备工作。
typedef libff::Fr<default_r1cs_gg_ppzksnark_pp> FieldT;
default_r1cs_gg_ppzksnark_pp::init_public_params();
接下来就需要明确「待证命题」是什么。这里不妨沿用之前的例子,证明秘密 x 满足等式 x^3 + x + 5 == out。这实际也是 Vitalik 博文 Quadratic Arithmetic Programs: from Zero to Hero 中用的例子。如果对下面的变化陌生,可尝试阅读该博文。
通过引入中间变量 sym_1、y、sym_2 将 x^3 + x + 5 = out 扁平化为若干个二次方程式,几个只涉及简单乘法或加法的式子,对应到算术电路中就是乘法门和加法门。你可以很容易地在纸上画出对应的电路。
x * x = sym_1
sym_1 * x = y
y + x = sym_2
sym_2 + 5 = out
通常文章到这里便会顺着介绍如何按照 R1CS 的形式编排上面的几个等式,并一步步推导出具体对应的向量。这对理解如何把 Gate 转换为 R1CS 有帮助,然而却不是本文的核心目的。所以此处省略一百字。
下面定义与命题相关的变量。首先创建的 protoboard 是 libsnark 中的一个重要概念,顾名思义就是原型板或者面包板,用来快速搭建电路,在 zk-SNARKs 电路中则是用来关联所有变量、组件和约束。接下来的代码定义了所有需要外部输入的变量以及中间变量。
// Create protoboard
protoboard<FieldT> pb;
// Define variables
pb_variable<FieldT> x;
pb_variable<FieldT> sym_1;
pb_variable<FieldT> y;
pb_variable<FieldT> sym_2;
pb_variable<FieldT> out;
下面将各个变量与 protoboard 连接,相当于把各个元器件插到“面包板”上。allocate() 函数的第二个 string 类型变量仅是用来方便 DEBUG 时的注释,方便 DEBUG 时查看日志。
out.allocate(pb, out);
x.allocate(pb, x);
sym_1.allocate(pb, sym_1);
y.allocate(pb, y);
sym_2.allocate(pb, sym_2);
pb.set_input_sizes(1);
注意,此处第一个与 pb 连接的是 out 变量。我们知道 zk-SNARKs 中有 public input 和 private witness 的概念,分别对应 libsnark 中的 primary 和 auxiliary 变量。那么如何在代码中进行区分呢?我们需要借助 set_input_sizes(n) 来声明与 protoboard 连接的 public/primary 变量的个数 n。在这里 n = 1,表明与 pb 连接的前 n = 1 个变量是 public 的,其余都是 private 的。
至此, 所有变量都已经顺利与 protoboard 相连,下面需要确定的是这些变量间的约束关系。这个也很好理解,类似元器件插至面包板后,需要根据电路需求确定他们之间的关系再连线焊接。如下调用 protoboard 的 add_r1cs_constraint() 函数,为 pb 添加形如 a * b = c 的 r1cs_constraint。即 r1cs_constraint<FieldT>(a, b, c) 中参数应该满足 a * b = c。根据注释不难理解每个等式和约束之间的关系。
// x*x = sym_1
pb.add_r1cs_constraint(r1cs_constraint<FieldT>(x, x, sym_1));
// sym_1 * x = y
pb.add_r1cs_constraint(r1cs_constraint<FieldT>(sym_1, x, y));
// y + x = sym_2
pb.add_r1cs_constraint(r1cs_constraint<FieldT>(y + x, 1, sym_2));
// sym_2 + 5 = ~out
pb.add_r1cs_constraint(r1cs_constraint<FieldT>(sym_2 + 5, 1, out));
至此,变量间的约束也已添加完成,针对命题的电路已构建完毕。下面进入前文提到的“四个步骤”中的第二步:使用生成算法(G)为该命题生成公共参数(pk 和 vk),即 trusted setup。生成出来的 proving key 和 verification key 分别可以通过 keypair.pk 和 keypair.vk 获得。
const r1cs_constraint_system<FieldT> constraint_system = pb.get_constraint_system();
const r1cs_gg_ppzksnark_keypair<default_r1cs_gg_ppzksnark_pp> keypair = r1cs_gg_ppzksnark_generator<default_r1cs_gg_ppzksnark_pp>(constraint_system);
进入第三步,生成证明。先为 public input 以及 witness 提供具体数值。不难发现,x = 3, out = 35 是原始方程的一个解。则依次为 x、out 以及各个中间变量赋值。
pb.val(out) = 35;
pb.val(x) = 3;
pb.val(sym_1) = 9;
pb.val(y) = 27;
pb.val(sym_2) = 30;
再把 public input 以及 witness 的数值传给 prover 函数进行证明,可分别通过 pb.primary_input() 和 pb.auxiliary_input() 访问。生成的证明用 proof 变量保存。
const r1cs_gg_ppzksnark_proof<default_r1cs_gg_ppzksnark_pp> proof = r1cs_gg_ppzksnark_prover<default_r1cs_gg_ppzksnark_pp>(keypair.pk, pb.primary_input(), pb.auxiliary_input());
最后我们使用 verifier 函数校验证明。如果 verified = true 则说明证明验证成功。
bool verified = r1cs_gg_ppzksnark_verifier_strong_IC<default_r1cs_gg_ppzksnark_pp>(keypair.vk, pb.primary_input(), proof);
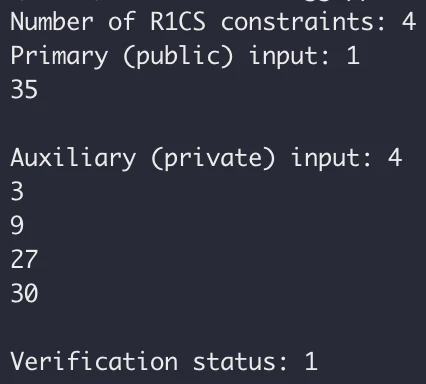
从日志输出中可以看出验证结果为 true,R1CS 约束数量为 4,public input 和 private input 数量分别为 1 和 4。日志输出符合预期。
实际应用中,trusted setup、prove、verify 会由不同角色分别开展,最终实现的效果就是 prover 给 verifier 一段简短的 proof 和 public input,verifier 可以自行校验某命题是否成立。对于前面的例子,就是能在不知道方程的解 x 具体是多少的情况下,验证 prover 知道一个秘密的 x 可以使得 x^3 + x + 5 = out 成立。
通过短短的几十行代码,你就可以很轻易地操控学术界 zk-SNARKs 最新研究成果。
5. 再次上手实践
经过上面的例子,我们已经了解了利用 libsnark 库开发 zk-SNARKs 电路的所有重要步骤。
现在不妨用新的例子来巩固一下:在不泄露秘密数字大小的前提下,证明数字小于 60。
这个在常规程序里用一个运算符就能完成的事情,在 libsnark 下面应该如何表示呢?
zk-SNARKs 电路开发的主要工作量和难点在于如何用代码“精确”地描述命题中的所有约束。一旦描述不“精确”,则要么是漏掉约束、要么是写错约束,最终电路想要证明的内容则会与原命题相差甚远。上一节的例子只涉及简单的乘法和加法,与 r1cs_constraint 最基本的形式一致,因此约束的表达相对容易。除此之外几乎所有的约束都不是很直观,作为初学者很难正确地描述约束细节。
幸好 libsnark 已经为我们实现了大量基础电路小组件。gadgetlib1 和 gadgetlib2 下提供了许多可以直接使用的 gadget。其中 gadgetlib1 更常用一些,里面收集了包括 sha256 在内的 hash 计算、merkle tree、pairing 等电路实现。
DangDangDang,gadgetlib1/gadgets/basic_gadgets.hpp 中的 comparison_gadget 正是我们所需。
comparison_gadget(protoboard<FieldT> pb,
const size_t n,
const pb_linear_combination<FieldT> A,
const pb_linear_combination<FieldT> B,
const pb_variable<FieldT> less,
const pb_variable<FieldT> less_or_eq,
const std::string annotation_prefix=)
该 gadget 需要传入的参数较多:n 表示位数,A 和 B 分别为需要比较的两个数,less 和 less_or_eq 用来标记两个数的关系是「小于」还是「小于或等于」。该 gadget 实现的原理简单来讲是把 A 和 B 的比较,转化为 2^n + B - A 按位表示。具体实现还用到了其余多个基础 gadget,可以通过 comparison_gadget<FieldT>::generate_r1cs_constraints() 研究。
这里需要创建以下变量,并将 x 和 max 与 pb 相连,把 max 值设为 60,代表数值上限。
protoboard<FieldT> pb;
pb_variable<FieldT> x, max;
pb_variable<FieldT> less, less_or_eq;
x.allocate(pb, x);
max.allocate(pb, max);
pb.val(max)= 60;
使用 comparison_gadget 创建 cmp,并把前面的参数填入,并调用 gadget 自带的 generate_r1cs_constraints() 方法。同时另外添加一个约束,要求 less * 1 = 1,也就是 less 必须为 true。
comparison_gadget<FieldT> cmp(pb, 10, x, max, less, less_or_eq, cmp);
cmp.generate_r1cs_constraints();
pb.add_r1cs_constraint(r1cs_constraint<FieldT>(less, 1, FieldT::one()));
输入 witness(秘密值 x),比如让 x = 18。这里还需要调用 comparison_gadget 的 generate_r1cs_witness 方法。
// Add witness values
pb.val(x) = 18; // secret
cmp.generate_r1cs_witness();
其余部分和上一个例子一致,即可在不泄露秘密数字大小的前提下,证明某数字小于 60。同理,就实现一个对数值作最大和最小值限定的 “range proof”。
在强大基础库的帮助下,我们又用更短的代码实现了证明需求。
6. Whats NEXT?
读到这里,相信大家都对 libsnark 的使用方法和 zk-SNARKs 电路开发有了一个初步的了解。
你或许已经发现,libsnark 的使用方法较简单,而真正的重点在于 zk-SNARKs 电路开发。正如前面提过的,必须用代码“精确”描述待证命题中的所有约束,“漏掉”或“写错”约束都会让证明内容与原本意图大相径庭,从而导致证明无意义。
如何正确高效地把真实业务逻辑转化为 zk-SNARKs 电路代码,这正是我们开发者需要不断研究和练习的。
好在我们已经有了一个 libsnark 试验场,可以很方便地自由修改、添加代码来尝试。
不论多复杂的电路实现,都是通过一个个更简单地「电路组件」组合封装而形成。因此 libsnark 自带的基础库是一个非常重要的学习资料——既要学习它们的使用方法,又要研究其实现原理。
我们也能通过阅读其他项目的电路实现来了解如何将 ZKP 应用到实际业务中,如 HarryR 的 ethsnarks-miximus 和 Loopring 的 protocol3-circuits。从这些项目中可以学习到如何工程化地开发更大规模的电路,以及与电路性能相关的各种设计优化细节,同时对电路约束规模会有更深刻的理解。
同时也欢迎大家继续关注安比实验室「零知识证明 Learn by Coding:libsnark 系列」后续文章,下次我们将尝试从 zk-SNARKs 与智能合约的结合、电路模块化开发、更复杂的 libsnark 实现案例、电路开发过程中容易踩的坑等角度来进一步讨论。
7. 附录
main.cpp
第一个例子 main.cpp,调用 libsnark 官方 example 的示例代码。通过该例子可了解 libsnark 的基本使用流程和主要函数。
#include <libff/common/default_types/ec_pp.hpp>
#include <libsnark/common/default_types/r1cs_gg_ppzksnark_pp.hpp>
#include <libsnark/relations/constraint_satisfaction_problems/r1cs/examples/r1cs_examples.hpp>
#include <libsnark/zk_proof_systems/ppzksnark/r1cs_gg_ppzksnark/r1cs_gg_ppzksnark.hpp>
using namespace libsnark;
/**
* The code below provides an example of all stages of running a R1CS GG-ppzkSNARK.
*
* Of course, in a real-life scenario, we would have three distinct entities,
* mangled into one in the demonstration below. The three entities are as follows.
* (1) The generator, which runs the ppzkSNARK generator on input a given
* constraint system CS to create a proving and a verification key for CS.
* (2) The prover, which runs the ppzkSNARK prover on input the proving key,
* a primary input for CS, and an auxiliary input for CS.
* (3) The verifier, which runs the ppzkSNARK verifier on input the verification key,
* a primary input for CS, and a proof.
*/
template<typename ppT>
bool run_r1cs_gg_ppzksnark(const r1cs_example<libff::Fr<ppT> > example)
{
libff::print_header(R1CS GG-ppzkSNARK Generator);
r1cs_gg_ppzksnark_keypair<ppT> keypair = r1cs_gg_ppzksnark_generator<ppT>(example.constraint_system);
printf(\n); libff::print_indent(); libff::print_mem(after generator);
libff::print_header(Preprocess verification key);
r1cs_gg_ppzksnark_processed_verification_key<ppT> pvk = r1cs_gg_ppzksnark_verifier_process_vk<ppT>(keypair.vk);
libff::print_header(R1CS GG-ppzkSNARK Prover);
r1cs_gg_ppzksnark_proof<ppT> proof = r1cs_gg_ppzksnark_prover<ppT>(keypair.pk, example.primary_input, example.auxiliary_input);
printf(\n); libff::print_indent(); libff::print_mem(after prover);
libff::print_header(R1CS GG-ppzkSNARK Verifier);
const bool ans = r1cs_gg_ppzksnark_verifier_strong_IC<ppT>(keypair.vk, example.primary_input, proof);
printf(\n); libff::print_indent(); libff::print_mem(after verifier);
printf(* The verification result is: %s\n, (ans ? PASS : FAIL));
libff::print_header(R1CS GG-ppzkSNARK Online Verifier);
const bool ans2 = r1cs_gg_ppzksnark_online_verifier_strong_IC<ppT>(pvk, example.primary_input, proof);
assert(ans == ans2);
return ans;
}
template<typename ppT>
void test_r1cs_gg_ppzksnark(size_t num_constraints, size_t input_size)
{
r1cs_example<libff::Fr<ppT> > example = generate_r1cs_example_with_binary_input<libff::Fr<ppT> >(num_constraints, input_size);
const bool bit = run_r1cs_gg_ppzksnark<ppT>(example);
assert(bit);
}
int main () {
default_r1cs_gg_ppzksnark_pp::init_public_params();
test_r1cs_gg_ppzksnark<default_r1cs_gg_ppzksnark_pp>(1000, 100);
return 0;
}
test.cpp
第二个例子 test.cpp。这个例子具体展示了如何利用 libsnark 构建一个最简单的电路。
#include <libsnark/common/default_types/r1cs_gg_ppzksnark_pp.hpp>
#include <libsnark/zk_proof_systems/ppzksnark/r1cs_gg_ppzksnark/r1cs_gg_ppzksnark.hpp>
#include <libsnark/gadgetlib1/pb_variable.hpp>
using namespace libsnark;
using namespace std;
int main () {
typedef libff::Fr<default_r1cs_gg_ppzksnark_pp> FieldT;
// Initialize the curve parameters
default_r1cs_gg_ppzksnark_pp::init_public_params();
// Create protoboard
protoboard<FieldT> pb;
// Define variables
pb_variable<FieldT> x;
pb_variable<FieldT> sym_1;
pb_variable<FieldT> y;
pb_variable<FieldT> sym_2;
pb_variable<FieldT> out;
// Allocate variables to protoboard
// The strings (like x) are only for debugging purposes
out.allocate(pb, out);
x.allocate(pb, x);
sym_1.allocate(pb, sym_1);
y.allocate(pb, y);
sym_2.allocate(pb, sym_2);
// This sets up the protoboard variables
// so that the first one (out) represents the public
// input and the rest is private input
pb.set_input_sizes(1);
// Add R1CS constraints to protoboard
// x*x = sym_1
pb.add_r1cs_constraint(r1cs_constraint<FieldT>(x, x, sym_1));
// sym_1 * x = y
pb.add_r1cs_constraint(r1cs_constraint<FieldT>(sym_1, x, y));
// y + x = sym_2
pb.add_r1cs_constraint(r1cs_constraint<FieldT>(y + x, 1, sym_2));
// sym_2 + 5 = ~out
pb.add_r1cs_constraint(r1cs_constraint<FieldT>(sym_2 + 5, 1, out));
const r1cs_constraint_system<FieldT> constraint_system = pb.get_constraint_system();
// generate keypair
const r1cs_gg_ppzksnark_keypair<default_r1cs_gg_ppzksnark_pp> keypair = r1cs_gg_ppzksnark_generator<default_r1cs_gg_ppzksnark_pp>(constraint_system);
// Add public input and witness values
pb.val(out) = 35;
pb.val(x) = 3;
pb.val(sym_1) = 9;
pb.val(y) = 27;
pb.val(sym_2) = 30;
// generate proof
const r1cs_gg_ppzksnark_proof<default_r1cs_gg_ppzksnark_pp> proof = r1cs_gg_ppzksnark_prover<default_r1cs_gg_ppzksnark_pp>(keypair.pk, pb.primary_input(), pb.auxiliary_input());
// verify
bool verified = r1cs_gg_ppzksnark_verifier_strong_IC<default_r1cs_gg_ppzksnark_pp>(keypair.vk, pb.primary_input(), proof);
cout << Number of R1CS constraints: << constraint_system.num_constraints() << endl;
cout << Primary (public) input: << pb.primary_input() << endl;
cout << Auxiliary (private) input: << pb.auxiliary_input() << endl;
cout << Verification status: << verified << endl;
}
range.cpp
第三个例子 range.cpp。该例子利用了 libsnark 自带的 comparison_gadget 来实现取值范围证明。
#include <libsnark/common/default_types/r1cs_gg_ppzksnark_pp.hpp>
#include <libsnark/zk_proof_systems/ppzksnark/r1cs_gg_ppzksnark/r1cs_gg_ppzksnark.hpp>
#include <libsnark/gadgetlib1/pb_variable.hpp>
#include <libsnark/gadgetlib1/gadgets/basic_gadgets.hpp>
using namespace libsnark;
using namespace std;
int main () {
typedef libff::Fr<default_r1cs_gg_ppzksnark_pp> FieldT;
// Initialize the curve parameters
default_r1cs_gg_ppzksnark_pp::init_public_params();
// Create protoboard
protoboard<FieldT> pb;
pb_variable<FieldT> x, max;
pb_variable<FieldT> less, less_or_eq;
x.allocate(pb, x);
max.allocate(pb, max);
pb.val(max)= 60;
comparison_gadget<FieldT> cmp(pb, 10, x, max, less, less_or_eq, cmp);
cmp.generate_r1cs_constraints();
pb.add_r1cs_constraint(r1cs_constraint<FieldT>(less, 1, FieldT::one()));
const r1cs_constraint_system<FieldT> constraint_system = pb.get_constraint_system();
// generate keypair
const r1cs_gg_ppzksnark_keypair<default_r1cs_gg_ppzksnark_pp> keypair = r1cs_gg_ppzksnark_generator<default_r1cs_gg_ppzksnark_pp>(constraint_system);
// Add witness values
pb.val(x) = 18; // secret
cmp.generate_r1cs_witness();
// generate proof
const r1cs_gg_ppzksnark_proof<default_r1cs_gg_ppzksnark_pp> proof = r1cs_gg_ppzksnark_prover<default_r1cs_gg_ppzksnark_pp>(keypair.pk, pb.primary_input(), pb.auxiliary_input());
// verify
bool verified = r1cs_gg_ppzksnark_verifier_strong_IC<default_r1cs_gg_ppzksnark_pp>(keypair.vk, pb.primary_input(), proof);
cout << Number of R1CS constraints: << constraint_system.num_constraints() << endl;
cout << Primary (public) input: << pb.primary_input() << endl;
cout << Auxiliary (private) input: << pb.auxiliary_input() << endl;
cout << Verification status: << verified << endl;
}










