Rust 智能合约养成日记(7)
1. 浮点数运算的精度问题
不同于常见的智能合约编程语言Solidity,Rust语言原生支持浮点数运算。然而,浮点数运算存在着无法避免的计算精度问题。因此,我们在编写智能合约时,并不推荐使用浮点数运算(尤其是在处理涉及到重要经济/金融决策的比率或利率时)。
目前主流计算机语言表示浮点数大多遵循了IEEE 754标准,Rust语言也不例外。如下是Rust语言中有关双精度浮点类型f64的说明与计算机内部二进制数据保存形式:
浮点数采用了底数为2的科学计数法来表达。例如可以用有限位数的二进制数 0.1101 来表示小数 0.8125,具体的转化方式如下:
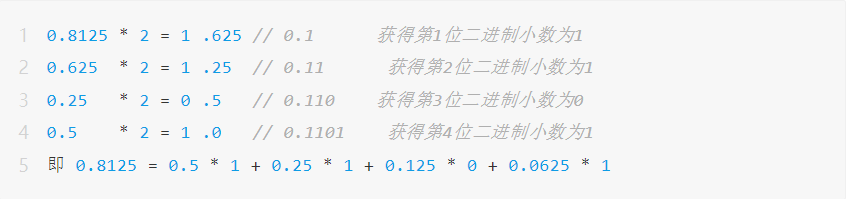
然而对于另一个小数 0.7来说,其实际转化为浮点数的过程中将存在如下问题:
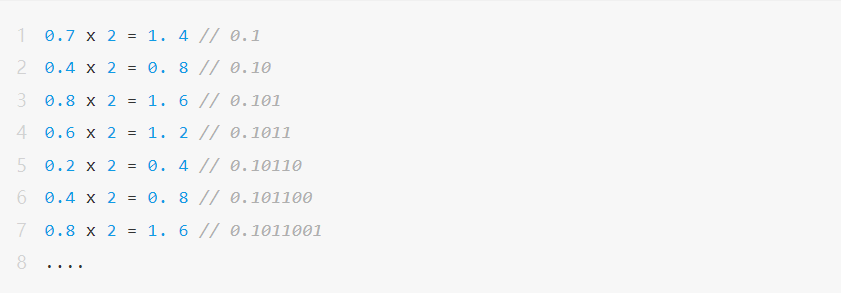
即小数 0.7 将表示为 0.101100110011001100.....(无限循环),无法用有限位长的浮点数来准确表示,并存在“舍入(Rounding)”现象。
假设在NEAR公链上,需要分发0.7个NEAR代币给十位用户,具体每位用户分得的NEAR代币数量将计算保存于result_0变量中。

执行该测试用例的输出结果如下:

可见在上述浮点运算中,amount的值并非准确地表示了0.7,而是一个极为近似的值0.69999999999999995559。进一步的,对于诸如amount/divisor的单一除法运算,其运算结果也将变为不精确的0.06999999999999999,并非预期的0.07。由此可见浮点数运算的不确定性。
对此,我们不得不考虑在智能合约中使用其它类型的数值表示方法,如定点数。
根据定点数小数点固定的位置不同,定点数有定点(纯)整数和定点(纯)小数两种。
小数点固定在数的最低位之后,则称其为定点整数
在实际的智能合约编写中,通常会使用一个具有固定分母的分数来表示某一数值,例如分数' x/N ',其中' N '是常数,' x '可以变化。
若“N”取值为“1,000,000,000,000,000,000”,也就是: ' 10^18 ',此时小数可被表示为整数,像这样:

在NEAR Protocol中,该N常见的取值为' 10^24 ',即 10^24 个yoctoNEAR等价于1个NEAR代币。
基于此,我们可以将本小节的单元测试修改为如下方式进行计算:
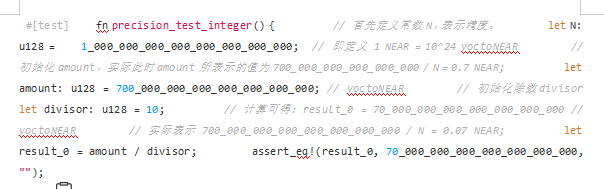
以此可获得数值精算的运算结果: 0.7 NEAR / 10 = 0.07 NEAR

2. Rust整数计算精度的问题
从上文第1小节的描述中可以发现,使用整数运算可解决某些运算场景中浮点数运算精度丢失问题。
但这并非意味着使用整数计算的结果完全是准确可靠的。本小节将介绍影响整数计算精度的部分原因。
2.1 运算顺序
同一算数优先级的乘法与除法,其前后顺序的变化可能直接影响到计算结果,导致整数计算精度的问题。
例如存在如下运算:

执行单元测试的结果如下:

我们可以发现result_0 = a * c / b 及 result_1 = (a / b)* c尽管它们的计算公式相同,但是运算结果却不同。
分析具体的原因为:对于整数除法而言,小于除数的精度会被舍弃。因此在计算result_1的过程中,首先计算的 (a / b) 会率先失去计算精度,变为0;而在计算result_0时,会首先算得a * c的结果20_0000,该结果将大于除数b,因此避免了精度丢失的问题,可得到正确的计算结果。
2.2 过小的数量级

该单元测试的具体结果如下:

可见运算过程等价的result_0和result_1运算结果并不相同,且result_1 = 13更加地接近于实际预期的计算值:13.3333....
3. 如何编写数值精算的Rust智能合约
保证正确的精度在智能合约中十分重要。尽管Rust语言中也存在整数运算结果精度丢失的问题,但我们可以采取如下一些防护手段来提高精度,达到令人满意的效果。
3.1 调整运算的操作顺序
令整数乘法优先于整数的除法。
3.2 增加整数的数量级
整数使用更大的数量级,创造更大的分子。
比如对于一个NEAR token来说,如果定义其上文所描述的N = 10,则意味着:若需要表示5.123的NEAR价值,则实际运算所采用的整数数值将表示为5.123* 10^10 = 51_230_000_000。该值继续参与后续的整数运算,可提高运算精度。
3.3 积累运算精度的损失
对于确实无法避免的整数计算精度问题,项目方可以考虑记录累计的运算精度的损失。
假设如下使用fn distribute(amount: u128, offset: u128) -> u128为USER_NUM位用户分发代币的场景。

在该测试用例中,系统每次将给3位用户分发10个Token。但是,由于整数运算精度的问题,第一轮中计算per_user_share时,获得的整数运算结果为10 / 3 = 3 ,即第一轮distribute用户将平均获得3个token,总计9个token被分发。
此时可以发现,系统中还剩下1个token未能分发给用户。为此可以考虑将该剩余的token临时保存在系统全局的变量offset中。等待下次系统再次调用distribute给用户分发token时,该值将被取出,并尝试和本轮分发的token金额一起分发给用户。
如下为模拟的代币分发过程:
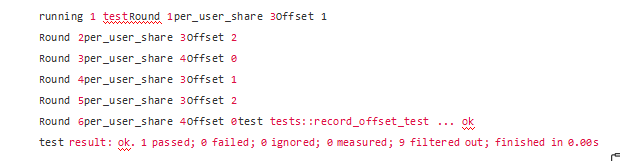
可见当系统开始第3轮地分发代币时,此时系统积累的offset值已达到2,该值将再次与本轮所要分发的10个token累加在一起,发放给用户。(本次计算 per_user_share = token_to_distribute / USER_NUM = 12 / 3 = 4将不存在精度损失。)
从整体上来看,在前3轮中,系统一共发放了30个Token。每个用户在每一轮中分别获得了 3、3、4个token,此时用户也总计获得30个token,达到了系统足额发放奖金目的。
3.4 使用 Rust Crate库 rust-decimal
该Rust库适用于需要有效精度计算和没有舍入误差的小数金融计算。
3.5 考虑舍入机制
在设计智能合约时,在舍入问题上,往往都采用“我要占便宜,他人不得薅我羊毛”的原则。根据这个原则,如果向下取整对我有利,则向下;如果向上取整对我有利,则向上;四舍五入不能确定是对谁有利,因此极少被采用。



