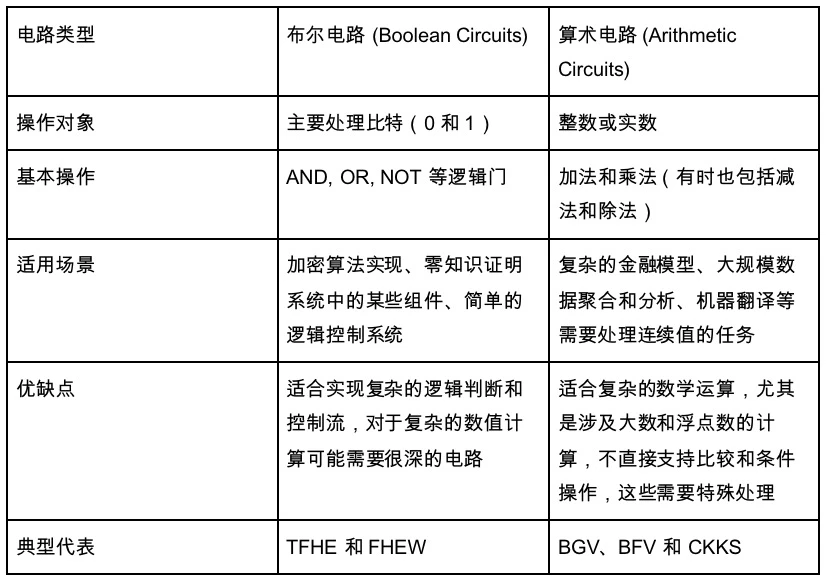
FHEとは
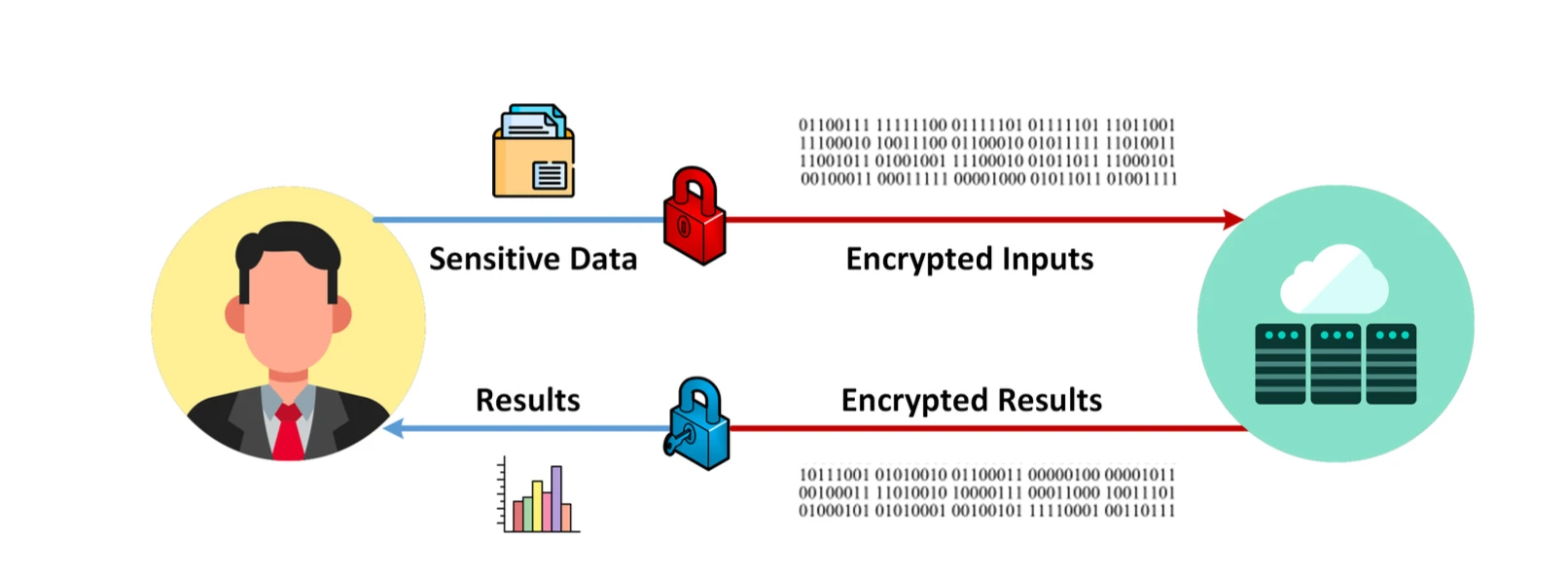
FHE プロセス、画像ソース: Data Privacy Made Easy
FHE (完全準同型暗号化) は、暗号化されたデータの直接計算をサポートする高度な暗号化テクノロジです。これは、プライバシーを保護しながらデータを処理できることを意味します。 FHE には、金融、医療健康、クラウド コンピューティング、機械学習、投票システム、モノのインターネット、ブロックチェーン プライバシー保護、その他の分野など、特にプライバシー保護の下でのデータ処理と分析に適用できるシナリオが数多くあります。しかし、実用化にはまだ一定の時間がかかるという課題があり、そのアルゴリズムによる計算量やメモリのオーバーヘッドが非常に大きく、スケーラビリティが低いことが挙げられます。次に、アルゴリズム全体の基本原理を簡単に説明し、この暗号アルゴリズムが直面する問題に焦点を当てます。
基本原則
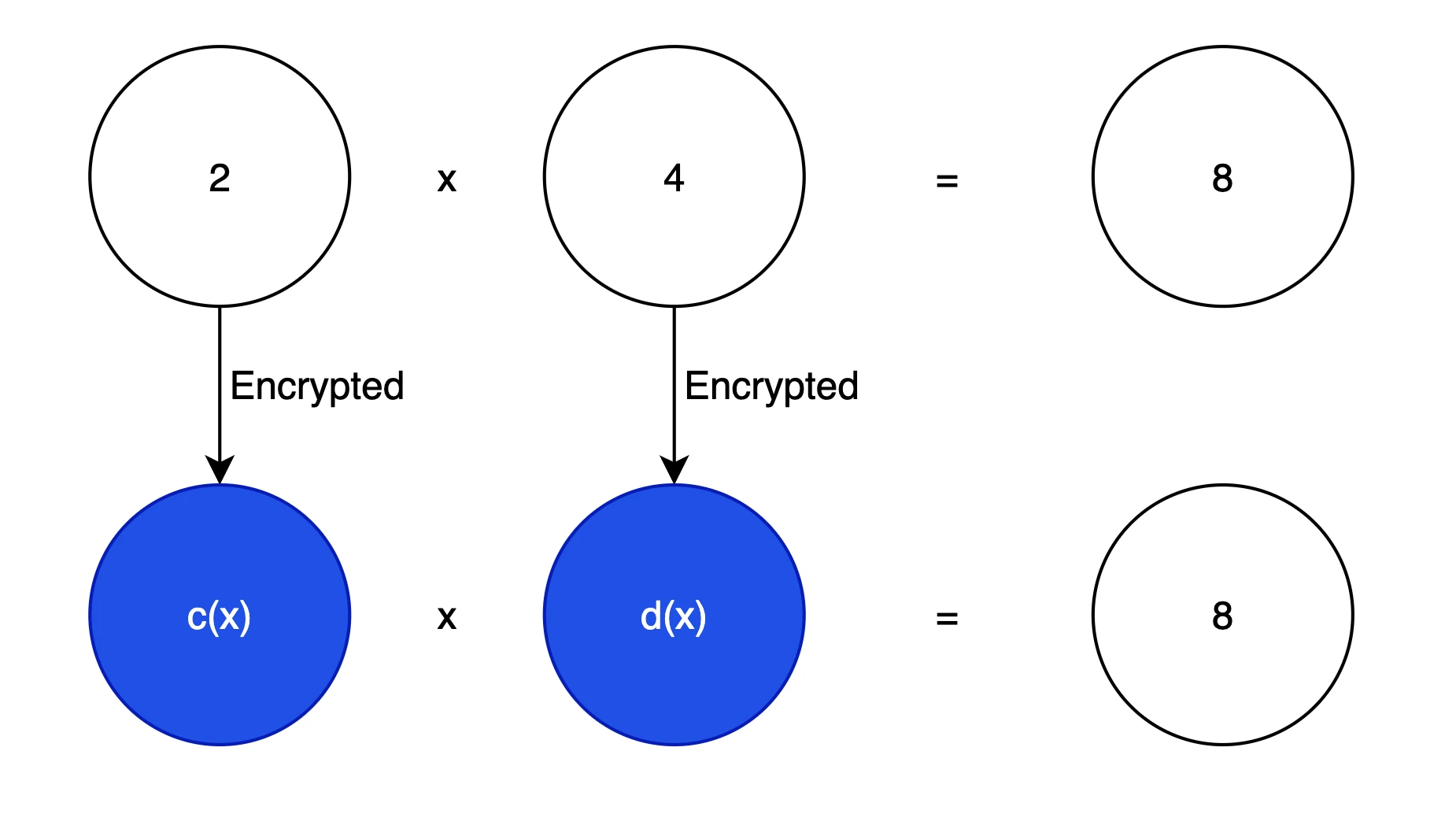
準同型暗号化アイコン
まず、暗号化されたデータに対して計算を実行しても同じ結果が得られる必要があります。これを上の図に示します。これが私たちの基本的な目標です。暗号化では、多項式は通常、元のテキストの情報を隠すために使用されます。多項式は線形代数問題に変換でき、ベクトル計算問題にも変換できるため、ベクトル用に高度に最適化された現代のコンピューターで演算を実行しやすくなります。並列計算として))、たとえば、3 x 2 + 2 x + 1 はベクトル [1, 2, 3] として表現できます。
単純化された HE システムで 2 を暗号化したいとします。次のようになります。
s(x) = 3 x 2 + 2 x + 1 などのキー多項式を選択します。
a(x) = 2 x 2 + 5 x + 3 などのランダムな多項式を生成します。
e(x) = -1 x + 2 などの小さな「間違った」多項式を生成します。
暗号化 2 -> c(x) = 2 + a(x)*s(x) + e(x)
なぜこれを行う必要があるのかについて話しましょう。暗号文 c(x) を取得したと仮定します。平文 m を取得したい場合、式は c(x) - e(x) - a(x) です。 *s(x) = 2、ここでのランダム多項式は a(x) が公開されていると仮定しているため、s(x) と c(x) がわかっている場合にのみ、キー s(x) が機密であることを確認する必要があります。誤差が非常に小さければ、理論的には無視でき、平文 m が得られます。
ここで最初の質問です。多項式はたくさんありますが、多項式はどのように選択すればよいでしょうか?最適な多項式の次数は何ですか?実際、多項式の次数は、HE の実装に使用されるアルゴリズムによって決まります。通常は、1024 / 2048 などの 2 のべき乗です。多項式の係数は、mod 10000 などの有限体 q からランダムに選択され、その後 0 ~ 9999 からランダムに選択されます。一様分布、離散ガウス分布など、係数のランダム選択には多くのアルゴリズムがあります。スキームが異なれば、通常、スキームの高速解法原理を満たすために、係数選択要件も異なります。
2番目の質問は、ノイズとは何ですか?すべての数値が s(x) であり、ランダム多項式がドメイン内にあると仮定すると、出力に従って平文 m が十分な回数入力される限り、特定のルールが存在するため、ノイズは攻撃者を混乱させるために使用されます。 c(x)、この2つのs(x)とc(x)の情報を判断することができます。ノイズ e(x) が導入されると、完全にランダムな小さな誤差が存在するため、単純な繰り返しの列挙では s(x) と c(x) を取得できないことが保証されます。このパラメータはノイズバジェットとも呼ばれます。 q = 2^32 と仮定すると、初期ノイズは約 2^3 になる可能性があります。いくつかの操作の後、ノイズは 2^20 まで増大する可能性があります。 2^20 << 2^32 であるため、この時点では復号化に十分なスペースがまだあります。
多項式を取得した後、c(x) * d(x) 演算を「回路」に変換する必要があります。これは主に、回路の抽象的な概念があらゆるものを表す一般的なコンピューティング モデルを提供するため、ZKP で頻繁に使用されます。計算と回路モデルにより、各操作によって発生するノイズの正確な追跡と管理が可能になり、SIMD モデルなどの高速計算のために、ASIC や FPGA などのプロフェッショナル ハードウェアへのその後の導入も容易になります。あらゆる複雑な演算を、加算や乗算などの単純なモジュール式回路要素にマッピングできます。

算術回路表現
加算と乗算は減算と除算、つまりあらゆる計算を表現できます。多項式の係数は 2 進数で表され、回路への入力と呼ばれます。各回路ノードは加算または乗算の実行を表します。 (*) は乗算ゲートを表し、(+) は加算ゲートを表します。これがアルゴリズム回路です。
ここで、意味情報が漏洩しないようにするために、ノイズと呼ばれる e(x) を導入します。私たちの計算では、加算により 2 つの e(x) 多項式が同じ次数の多項式に変わります。乗算では、2 つのノイズ多項式を乗算すると、e(x) の次数とテキストのサイズが指数関数的に増加します。ノイズが大きすぎると、結果の計算中にノイズを無視できなくなり、元のテキスト m が大きくなります。復元できません。これは、ノイズが指数関数的に増大し、すぐに使用不可能なしきい値に達するため、HE アルゴリズムが任意の計算を表現する能力を制限する主な理由です。回路ではこれを回路の深さといい、乗算の回数が回路の深さの値となります。
準同型暗号 HE の基本原理を上の図に示します。準同型暗号を制限するノイズ問題を解決するために、いくつかの解決策が提案されています。
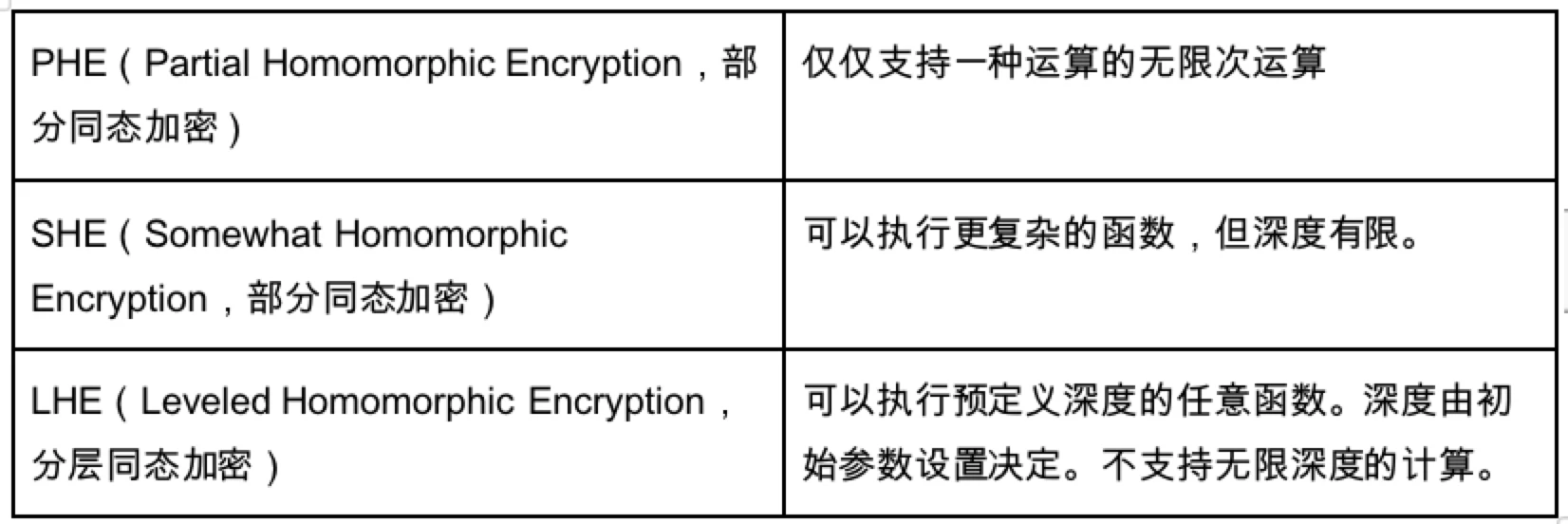
LHE はここでは非常に適したアルゴリズムです。このアルゴリズムでは、深さが決定されている限り、その深さ内で任意の関数を実行できますが、PHE と SHE はチューリング完全性を達成できません。したがって、これに基づいて、暗号学者は研究を実施し、FHE 完全準同型暗号を構築するための 3 つのテクノロジーを提案し、無限の深さで任意の関数を実行するというビジョンを実現することを望んでいます。
キーの切り替え: 乗算後、暗号文のサイズは指数関数的に増大するため、その後の操作でメモリとコンピューティング リソースが大幅に要求されます。そのため、各乗算の後にキーの切り替えを実装すると、暗号文を圧縮できますが、多少のノイズが発生します。 。
係数の切り替え: 乗算でもキーの切り替えでも、ノイズは指数関数的に増加します。係数 q は、先ほど説明した Mod 10000 であり、パラメータは [0, 9999] でのみ取得できます。複数の計算の後、最終的なノイズは依然として q 内にあり、復号化できます。したがって、複数の操作の後、ノイズ指数がしきい値を超えて増加するのを防ぐために、モジュラススイッチングを使用してノイズバジェットを削減し、ノイズを抑制する必要があります。ここで基本原理を得ることができます。計算が複雑で回路の深さが大きい場合、複数回の指数関数的な増加後の可用性に対応するには、より大きなモジュラス q ノイズ バジェットが必要になります。
ブートストラップ: しかし、無限の深度計算を実現したい場合、モジュラスはノイズの増加を制限することしかできませんが、各スイッチによって q 範囲が小さくなることがわかり、それは計算の複雑さを軽減する必要があることを意味します。減りました。ブートストラップは、ノイズを低減するのではなく、ノイズを元のレベルにリセットするリフレッシュ テクノロジです。ブートストラップではモジュラスを下げる必要がないため、システムの計算能力を維持できます。ただし、多くのコンピューティング リソースが必要になるという欠点があります。
一般に、限られたステップでの計算の場合、モジュラス スイッチングを使用するとノイズを減らすことができますが、モジュラス、つまりノイズ バジェットも減少するため、コンピューティング能力が圧縮されます。したがって、これは限られたステップでの計算のみに当てはまります。 Bootstrap はノイズ リセットを実装できるため、LHE アルゴリズムに基づいて真の FHE、つまり任意の関数の無限計算を実現できます。これが Fully of FHE の意味でもあります。
ただし、大量のコンピューティング リソースを必要とするという欠点も明らかです。そのため、通常の状況では、これら 2 つのノイズ低減テクノロジが組み合わせて使用され、遅延によりブートストラップ時間がかかります。モジュラス切り替えではノイズをさらに効果的に制御できない場合は、より計算コストの高いブートストラップが使用されます。
現在の FHE ソリューションには次の特定の実装があり、そのすべてでブートストラップ コア テクノロジが使用されています。
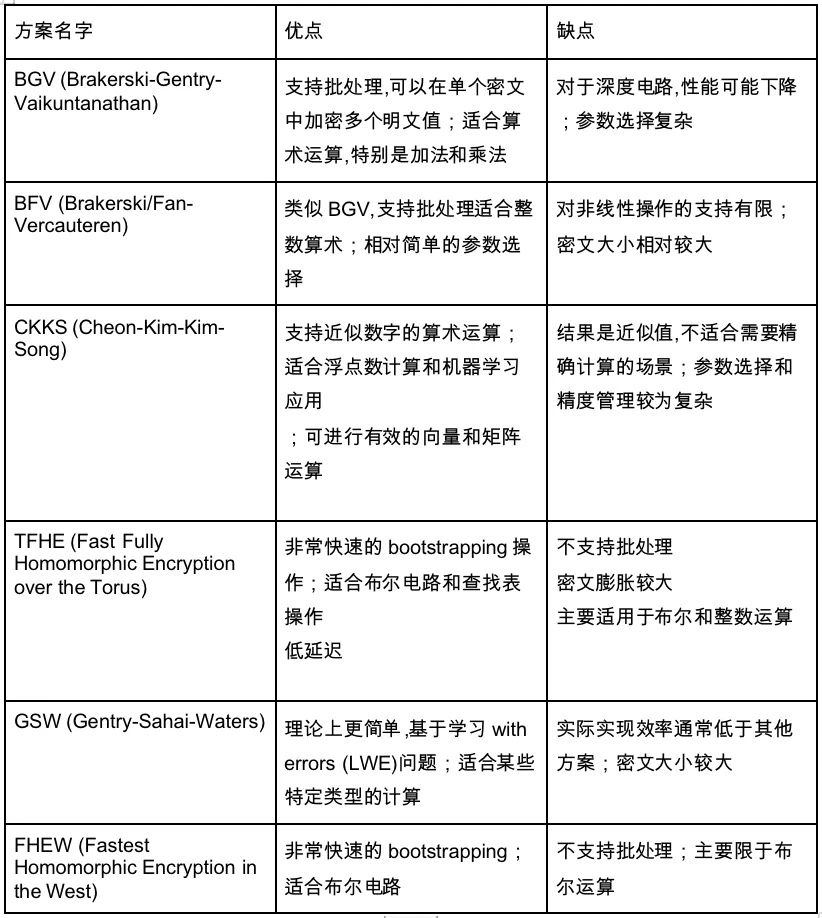
これは、上で紹介しなかった種類の回路にもつながります。主なものは演算回路です。しかし、別の種類の回路、ブール回路もあります。算術回路は 1+1 のような比較的抽象的なものですが、ブール回路内のすべての数値は基数 01 に変換され、すべてのノードは NOT、OR、AND 演算を含むブール演算です。私たちのコンピュータの回路実装と似ています。演算回路は抽象回路です。
したがって、非常に大まかに言って、ブール演算はデータ集約度が低い柔軟な処理であるのに対し、算術演算はデータ集約型アプリケーション向けのソリューションであると考えることができます。
FHEが直面する問題
計算を暗号化してから「回路」に変換する必要があり、単純な計算では2+4を計算するだけなので、暗号化後は暗号による間接的な計算プロセスが多数導入されており、ノイズ問題を解決するためにブートストラップとして使用すると、計算コストが通常の計算よりも N 桁高くなります。
実世界の例を使用して、コンピューティング リソースに対するこれらの追加の暗号化プロセスのオーバーヘッドを読者に感じてもらいます。 3 GHz プロセッサで通常の計算に 200 クロック サイクルかかると仮定すると、通常の AES-128 復号化には約 67 ナノ秒 (200/3 GHz) かかります。 FHE バージョンの所要時間は 35 秒で、通常バージョン (35/67 e-9) の約 5 億 2,238 万 8,060 倍です。つまり、同じ計算資源、同じ通常のアルゴリズムとFHE計算時のアルゴリズムを使用すると、計算資源要件は約5億回となる。

DARPA dprive プログラム、出典: DARPA
データセキュリティの目的で、米国の DARPA は 2021 年に特別に Dprive プログラムを構築し、マイクロソフト、インテルなどを含む複数の研究チームを招待しました。彼らの目標は、FHE のコンピューティング速度を向上させるための FHE アクセラレータとサポート ソフトウェア スタックを作成することです。暗号化されていないデータに対して同様の操作を行うことで、FHE の計算速度が通常の計算の約 1/10 になるという目標を達成します。 DARPA プログラムマネージャーの Tom Rondeau 氏は、「FHE の世界では、私たちの計算はプレーンテキストの世界よりも約 100 万倍遅いと推定されています。
Dprive は主に次の側面に焦点を当てています。
プロセッサのワード長を増やす: 最新のコンピュータ システムは 64 ビットのワード長を使用します。つまり、数値は最大 64 ビットまで可能ですが、実際には、q は 1024 ビットになることが多く、これを実現したい場合は、q を分割する必要があります。メモリリソースに影響を及ぼし、速度が低下します。したがって、より大きな q を実現するには、1024 ビット以上のワード サイズのプロセッサを構築する必要があります。前述したように、有限体 q は非常に重要であり、それが大きいほど、より多くのステップを計算できるため、全体的なコンピューティング リソースの消費が削減されます。 q は FHE で中心的な役割を果たし、セキュリティ、パフォーマンス、実行可能な計算量、必要なメモリ リソースなど、スキームのほぼすべての側面に影響を与えます。
ASIC プロセッサの構築: 前述したように、並列化の容易さなどの理由から、多項式を構築し、多項式を介して回路を構築しました。これは ZK と似ています。現在の CPU と GPU には、回路を実行するためのこの機能 (コンピューティング リソースとメモリ リソース) が備わっておらず、FHE アルゴリズムを使用できるように専用の ASIC プロセッサを構築する必要があります。
並列アーキテクチャ MIMD を構築します。 SIMD 並列アーキテクチャとは異なり、SIMD は複数のデータに対して 1 つの命令、つまりデータ分割と並列処理のみを実行できますが、MIMD はデータを分割し、計算に異なる命令を使用できます。 SIMD は主にデータの並列処理に使用され、ほとんどのブロックチェーン プロジェクトにおけるトランザクションの並列処理の主要なアーキテクチャでもあります。 MIMD はさまざまな種類の並列タスクを処理できます。 MIMD は技術的により複雑であり、同期と通信の問題に重点を置く必要があります。
DARPA の DEPRIVE プログラムの終了まであと 1 か月しかありません。Dprvie の当初の計画は 2021 年に開始され、2024 年 9 月に 3 段階の計画が終了する予定でした。しかし、その進捗は遅く、まだ期待に達していないようです。通常の計算に比べて1/10の効率を目標とします。
FHE 技術の進歩は ZK 技術と同様に遅いですが、ハードウェア実装が技術実装の前提条件であるという深刻な問題に直面しています。しかし、長期的には、特に最初の部分に挙げた一部の安全なデータのプライバシーを保護するという点で、FHE テクノロジーには独自の重要性があると私たちは依然として信じています。 DARPA にとって、国防総省は大量の機密データを保有しており、AI の一般的な機能を軍に公開したい場合は、データ セキュリティの形で AI を訓練する必要があります。それだけでなく、医療や金融などの重要な機密データにも適用できます。実際、FHE はすべての通常の計算には適していませんが、この種のセキュリティは特に重要です。ポスト量子の時代。
このような最先端技術の場合、投資サイクルから事業化までの時間差を考慮する必要があります。したがって、FHE の実装時期については十分に注意する必要があります。
ブロックチェーンの組み合わせ
ブロックチェーンでは、FHE は主にデータのプライバシーを保護するためにも使用され、その応用分野には、オンチェーンのプライバシー、AI トレーニング データのプライバシー、オンチェーンの投票プライバシー、オンチェーンのプライバシー トランザクション レビューなどが含まれます。その中でも、FHE はオンチェーン MEV ソリューションの候補の 1 つとしても知られています。 MEV の記事「暗い森を照らす - MEV の謎を明らかにする」によると、現在の MEV ソリューションの多くは、MEV アーキテクチャを再構築する単なる手段であり、解決策ではありません。実際、サンドイッチ攻撃は UX の問題を引き起こしており、まだ解決されていません。私たちが最初に考えた解決策は、ステータスを公開したままトランザクションを直接暗号化することでした。
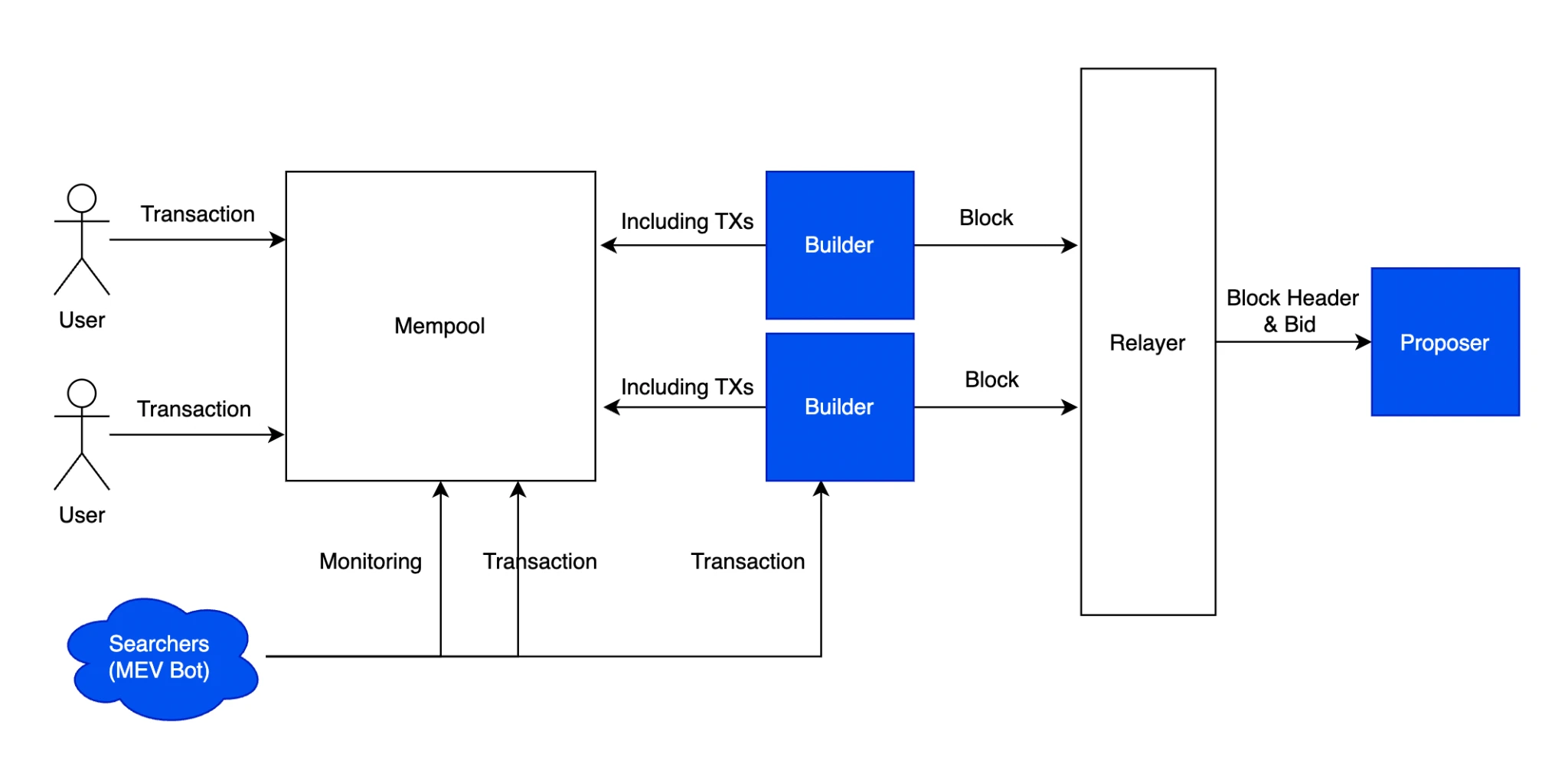
MEV PBS プロセス
しかし、トランザクションを完全に暗号化すると、MEV ボットによってもたらされるプラスの外部性が同時に消滅してしまうという問題もあります。FHE を実行するには、検証者ビルダーが仮想マシン上で実行される必要があり、検証者もまた、最終状態が正しいかどうかを確認するには、ノードを実行するための要件が大幅に増加し、ネットワーク全体のスループットが 100 万分の 1 に低下します。
主なプロジェクト
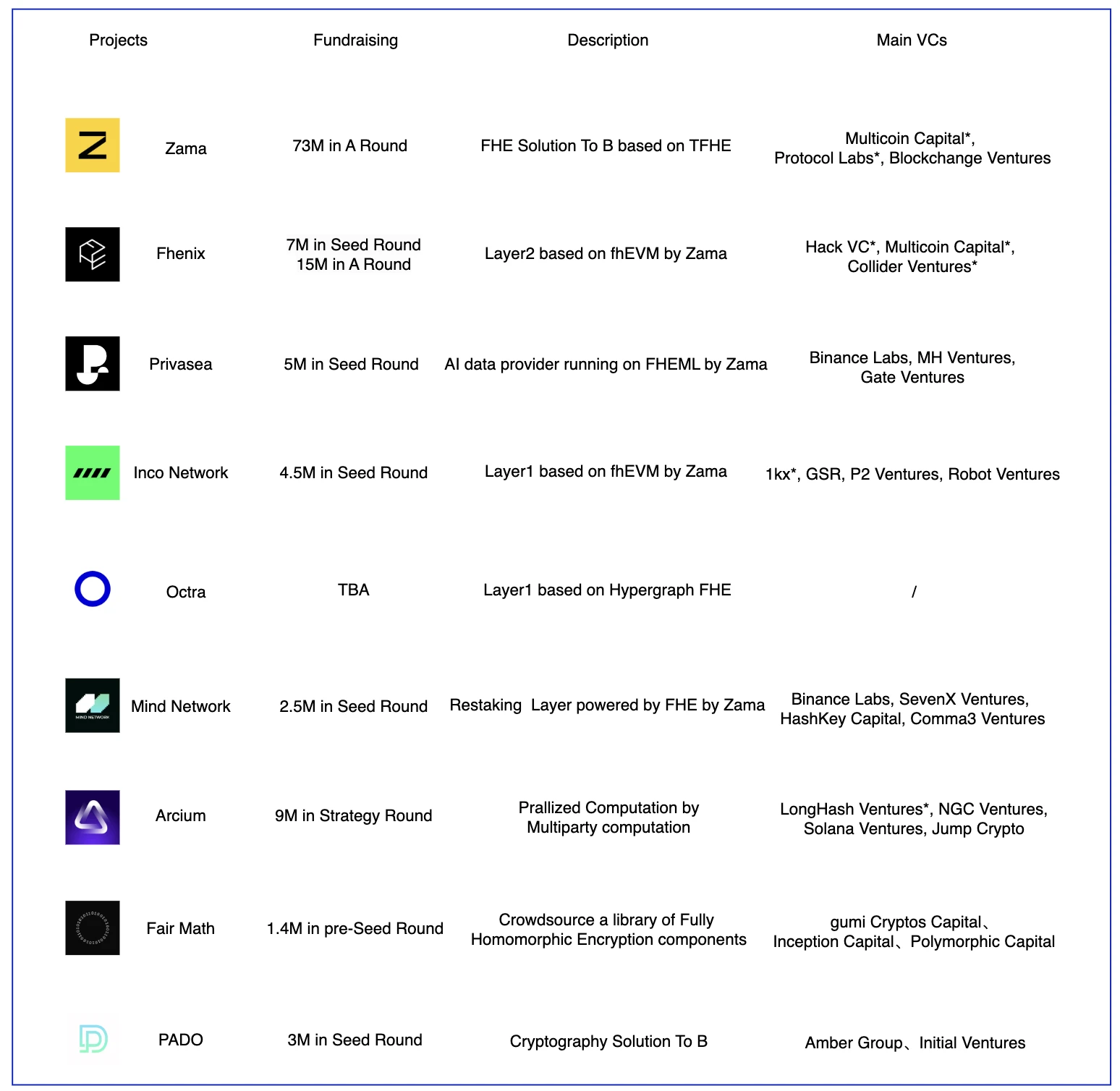
FHEの風景
FHE は比較的新しいテクノロジーであり、現在プロジェクトで使用されている FHE テクノロジーのほとんどは、Fhenix、Privasea、Inco Network、Mind Network など、Zama によって構築されています。これらのプロジェクトでは、座間のFHEエンジニアリング実装能力が認められました。上記のプロジェクトのほとんどは、Zama が提供するライブラリに基づいて構築されています。主な違いはビジネス モデルにあります。 Fhenix はプライバシー優先の Optimism Layer 2 を構築したいと考えており、Privasea は FHE の機能を使用して LLM データ操作を実行したいと考えていますが、これは非常に大量のデータを必要とする操作であり、FHE には非常に高い技術要件とハードウェア要件が必要です。 TFHE に基づくのは最適な選択ではない可能性があります。 Inco Network と Fhenix は両方とも fhEVM を使用しますが、1 つはレイヤー 1 で構築され、もう 1 つはレイヤー 2 で構築されます。 Arcium は、FHE、MPC、ZK などの複数の暗号化テクノロジーの融合に基づいて構築されています。 Mind Network のビジネス モデルはまったく異なり、流動性セキュリティと FHE に基づくサブネット アーキテクチャを提供することで、経済的セキュリティとコンセンサス層での投票の信頼の問題を解決するために、再ステーキング トラックを選択しました。
座間市
Zama は TFHE に基づくソリューションであり、ブール演算と低語長の整数演算の処理に重点を置いたブートストラップ テクノロジの使用を特徴としています。FHE ソリューションよりも高速な技術実装ではありますが、それでもまだ劣っています。第二に、データ集約型のタスクに直面すると、回路の深さが大きすぎて処理できなくなります。これはデータ集約型のソリューションではなく、暗号化プロセスの特定の重要なステップにのみ適用されます。
TFHE には現在、既成の実装コードがあります。Zama の主な仕事は、その rs-TFHE クレートである Rust 言語を使用して TFHE を書き直すことです。同時に、ユーザーが Rust を使用する敷居を下げるために、Python を rs-TFHE 相当のものに変換できるトランスコンパイル ツール Concrate も構築しました。このツールを使用すると、Python に基づく大規模なモデル言語を TFHE-rs に基づく Rust 言語に翻訳できます。この方法では、準同型暗号化に基づく大規模なモデルを実行できますが、現時点ではデータ集約型のタスクは実際には TFHE シナリオには適していません。ザマの製品 fhEVM は、完全準同型暗号化 (FHE) を使用して EVM 上に機密スマート コントラクトを実装するテクノロジーであり、Solidity 言語に基づいてコンパイルされたエンドツーエンドの暗号化スマート コントラクトをサポートできます。
一般に、To B 製品として、Zama は TFHE に基づいて比較的完全なブロックチェーン + AI 開発スタックを構築しました。これは、Web3 プロジェクトが FHE インフラストラクチャとアプリケーションを簡単に構築するのに役立ちます。
オクトラ
Octra の特別な点は、FHE の実装に別のテクノロジーを使用していることです。ハイパーグラフと呼ばれるテクノロジーを使用してブートストラップを実装します。これもブール回路に基づいていますが、Octra では、ハイパーグラフに基づくテクノロジーにより、より効率的な FHE を実現できると考えています。これは、FHE を実装するための Octra の独自のテクノロジーであり、チームは非常に強力なエンジニアリングおよび暗号化能力を備えています。
Octra は、OCaml、AST、ReasonML (Octra ブロックチェーン ネットワークと対話するスマート コントラクトおよびアプリケーション用に特別に設計された言語)、C++ などのコード ライブラリを使用して開発された新しいスマート コントラクト言語を構築しました。 Hyperggraph FHE ライブラリが構築するものは、あらゆるプロジェクトと互換性があります。
そのアーキテクチャは、Mind Network、Bittensor、Allora などのプロジェクトにも似ています。メイン ネットワークを構築し、他のプロジェクトがサブネットとなって相互に分離された動作環境を構築します。同時に、これらのプロジェクトと同様に、アーキテクチャ自体により適した新しいコンセンサス プロトコルを構築しました。Octra は、基本的に DAG (有向非巡回グラフ) に基づいた、機械学習に基づくコンセンサス プロトコル ML コンセンサスを構築しました。 。
このコンセンサスの技術原則はまだ明らかにされていませんが、大まかに推測することはできます。おそらくトランザクションはネットワークに送信され、SVM (サポート ベクター マシン) アルゴリズムを使用して、主に各ノードの現在のネットワーク負荷に基づいて最適な処理ノードが決定されます。システムは、履歴データ (ML アルゴリズム学習) に基づいて最適な親ノードのコンセンサス パスを決定します。ノードの 1/2 が満たされていれば、増大するデータベースについて合意に達することができます。
期待する
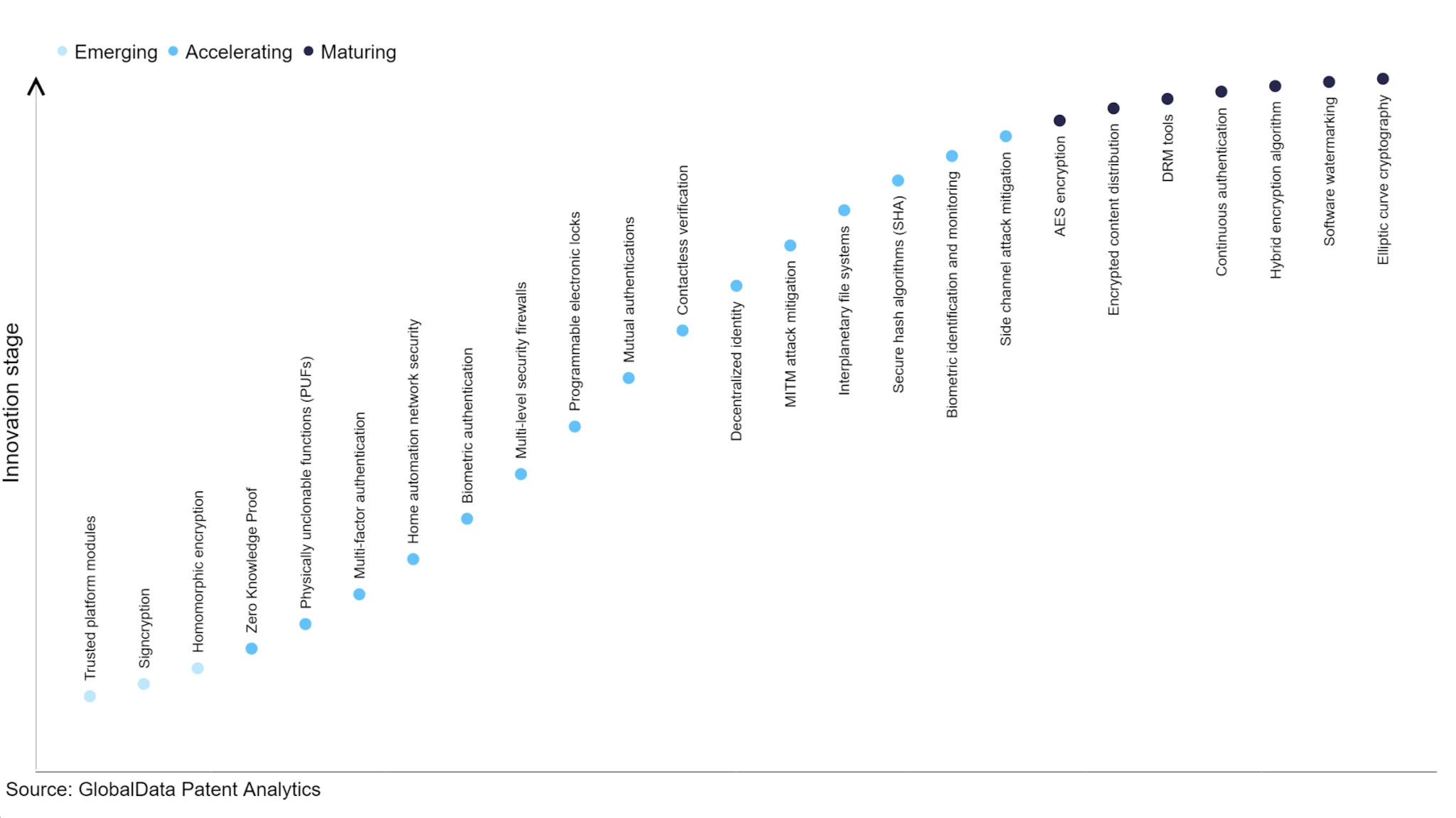
最先端の暗号技術の開発状況、出典: Verdict
FHE テクノロジーは未来志向のテクノロジーであり、その開発状況は ZK テクノロジーに比べてまだ劣っており、プライバシー保護による効率の低さとコストの高さのため、ほとんどの営利組織は十分な意欲を持っていません。 Crypto VC の投資により、ZK テクノロジーの開発はより速くなりました。 FHEはまだ非常に初期段階にあり、コストが高く、エンジニアリングの難易度が高く、商業化の見通しが不透明であるため、現在でも市場に出ているプロジェクトはほとんどありません。 2021 年、DAPRA はインテルやマイクロソフトなどの複数の企業と提携して 42 か月の FHE 攻撃計画を開始しましたが、ある程度の進歩はありましたが、達成されたパフォーマンス目標にはまだ程遠いです。 Crypto VCがこの方向に注目するにつれて、より多くの資金がこの業界に流入し、ZamaやOctra Aなどの強力なエンジニアリングと研究能力を備えたプロジェクトも増えることが予想されます。有能なチームが舞台の中心に立っている。FHE テクノロジーとブロックチェーンの商用化および開発状況の組み合わせは、まだ検討する価値がある。現時点での最良のアプリケーションは検証ノード投票の匿名化であるが、その適用範囲はまだ狭い。
ZK と同様に、FHE チップの実装は FHE の商用化の前提条件の 1 つであり、現在、Intel、Chain Reaction、Optalysys などの多くのメーカーがこの点を検討しています。 FHE は多くの技術的抵抗に直面していますが、FHE チップの実装により、完全準同型暗号化は大きな期待と正確な需要を持つ技術として、国防、金融、医療などの業界に大きな変化をもたらし、その可能性を解放します。これらのプライベートデータを将来の量子アルゴリズムなどのテクノロジーと組み合わせることで、爆発的な瞬間が到来するでしょう。
商業化可能な FHE 製品を構築している場合、またはより最先端の技術革新をお持ちの場合は、この初期の最先端テクノロジーを喜んで調査します。










