TL;DR
在上一篇文章 Hello, OlaVM! 中提到,OlaVM 的愿景是建立一个高性能的 ZKVM,本文将重点介绍使得 OlaVM 获得高性能的工具之一,Lookup argument。Lookup argument 对缩减电路规模,以提高 ZK 效率有很重要的作用,在 ZKVM 的电路设计中被广泛应用,通过本篇文章你可以了解到:
1.Lookup argument 在 ZKVM 中将发挥着怎样的角色?
2.Plookup 协议原理。
3.Halo 2 的 Lookup argument协议原理。
4.两个 Lookup argument 算法之间的联系。
The roles in ZKVM
所谓的 ZKVM,其实就是用 ZK 约束 VM 所有的执行过程,VM 的执行过程一般可以分为:指令执行,内存访问,内置函数执行等。在一个 trace 里执行对这些操作的约束看起来有点不切实际,首先,不同操作类型的约束对应不同的 trace 的宽度,如果其中一个约束对应的 trace 宽度特别大,就会造成其余约束对应 trace 的浪费;然后,一个 trace 里有太多不同的操作类型,就会引入更多的 selector,不仅会增加多项式的个数,而且还会增加约束的阶;最后,由于群的阶限制,trace 的行数不能超过这个群的阶,因此,应该尽量减少某种类型的操作所占用的 trace 行数。
因此,为了简单,我们需要:
a.把不同的操作类型分成多个子 trace,然后分别证明,主 trace 和子 trace 之间需要通过 Lookup argument 来保证数据的一致性。
b.对于一些 ZK-unfriendly 计算,我们可以通过 Lookup argument 技术来缩减 trace 的规模,比如位运算等。
当然,也有其他的一些技术手段来减少 trace 规模,我们将在后面的文章中给予说明。
Lookup between trace tables
VM 所有的执行过程会组成一个完整的 trace,称为主 trace,这里的完整是包含 VM 执行的所有状态,不会涉及到辅助状态,比如,方便 ZK 验证的一些扩展信息等;如前面所述,在主 trace 里面包含这种辅助信息,会使得主 trace 变得复杂,难于约束。因此,为了约束方便,通常会建立一些子 trace,然后分别针对这些子 trace 进行约束,而主 trace 主要用来进行执行正确的程序约束和 Context 约束。

图片 1. Lookup between traces
通过建立不同的子 trace,我们把 VM 执行的不同操作进行划分,通过 Lookup argument 技术来保证了子 trace 的数据源于主 trace。对于子 trace 里的数据有效性证明,需要根据具体的操作类型,生成不同的 trace,然后用对应的约束去证明 trace 的有效性;特别是对于 bitwise,rangcheck 等 zk-unfriendly 操作。
Lookup for ZK-unfriendly operations
如前面所述,每个子 trace 的证明是独立的,所以获得一个尽可能小的 trace,会提高 prover 的效率。以 bitwise 为例,bitwise 操作包含 AND, XOR, NOT 三种操作。如果想通过电路单纯的实现对 bitwise 操作的约束,那需要做的可能是,把每个 op 拆成多个 2 进制的 limbs,如果这些 op 是 3 2bit 位宽,那就会拆分成 32 个 limbs。然后,你需要约束:
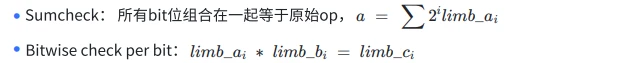
总共占用 3 + 32 * 3 = 99 个 trace cell,约束个数为 3 次 sumcheck + 32 次 bitwise = 35 个。
如果这个时候有一些真值表,对于 AND, XOR, NOT 计算,你可以定义三个表,这些表里存的是指定位宽的 op 进行 bitwise 计算的数据,比如 8 bit。对于 3 2bit 的 op,只需要把它们拆分成 4 个 8 bit 的 limbs,然后这些 op 的 limbs 之间的 bitwise 关系,也不用对应的约束去实现,只需要在 fixed table 里进行 Lookup 即可,此时,总共占用了 3+ 4 * 3 = 15 个 trace cell, 约束个数为 3 次 sumcheck + 1 次 Lookup argument(支持 Batch Looup)。

图 2. Lookup in Arithmetic operations
Lookup argument 不仅对 bitwise 操作的证明有极大的提升作用,对于 rangeck 操作同样。对于 3 2bit 的 op,只需要把他拆分成 2 个 16 bit 的 limbs 即可;这里有两个很好的设计,一个是会使得 rangecheck 占用更少的 trace cells;另外一个是 rangcheck 的 sum 约束可以复用我们自定义的 ADD-MUL 约束。对于不同的计算类型,能够复用同一个约束,对整体的效率提升具有很大的帮助,如上图所示,对于自定义的 ADD-MUL gate,它可以支持 ADD, MUL, ADD-MUL, EQ, RANGECHECK 五种计算类型的约束复用。
Plookup 协议
介绍

符号说明

预处理

协议过程

协议理解




Halo 2 Lookup 协议
介绍

协议过程

支持 ZK

Extend - 1 : Vector Lookup

Extend - 2 : Multi-tables

Links between Plookup and Lookup
Plookup 协议与 Halo 2 的 lookup 协议都能证明 f⊂t ,但两个协议的思想是不同的,区别如下:
Plookup 需要使用 f 和 t 构建一个新的数列 s , f 和 t 中的元素都在 s 中至少出现一次,接着通过比较 s 和 t 中元素的非零距离集合是相等的来证明 s⊂t,最终 f⊂s⊂t→f⊂t 。
Halo 2 的 lookup 直接证明 f⊂t ,不需要构建新的数列,比 plookup 更简洁。
Plookup 和 Halo 2 lookup 都需要对集合进行排序和补齐,plookup 补齐后 |t|=|f|+ 1 ,Halo 2 lookup 补齐后 |t|=|f|= 2 ^k 。
参考
1.Hello, OlaVM!:https://hackmd.io/@sin 7 y/H 1 yPj_J 8 i
2.OlaVM:https://olavm.org/
3.Plookup 协议:https://eprint.iacr.org/2020/315.pdf
4.Halo 2 的 Lookup argument:https://zcash.github.io/halo 2/design/proving-system/lookup.html
关于我们
Sin 7 y 成立于 2021 年,由顶尖的区块链开发者组成。我们既是项目孵化器也是区块链技术研究团队,探索 EVM、Layer 2、跨链、隐私计算、自主支付解决方案等最重要和最前沿的技术。团队于 2022 年 7 月推出 OlaVM 白皮书,致力于打造首个快速、可扩展且兼容 EVM 的 ZKVM。
官网:https://sin 7 y.org/
白皮书:https://olavm.org/
社群:http://t.me/sin 7 y_labs
官推:@Sin 7 y_Labs
微信公众号:Sin 7 y
邮箱:contact@sin 7 y.org
研究文章(EN):https://hackmd.io/@sin 7 y
Github:Sin 7 y










