
In a blockchain network, how do nodes ensure that all data for newly proposed blocks is available? Why is this important?
In this article, we’ll take a deep dive into the data availability issue and how it affects Ethereum’s scalability.
What are the data availability issues?
Data Availability (DA) Problem: How do nodes in a blockchain network ensure that all data in newly proposed blocks is actually available? If the data is not available, the block may contain malicious transactions hidden by the block producer. Even if a block contains non-malicious transactions, hiding them could threaten the security of the system.
For example, assume Alice is a ZK-Rollup operator. She submitted a ZK-Proof on Ethereum and it was verified. If she does not submit all transaction data on Ethereum, users of the rollup may still be in the dark about their current account balances, although her proof confirms that all state transitions made in the rollup are valid. Because of the zero-knowledge nature, the submitted proof cannot reveal information about the current state.
There is a similar example in the Optimistic Rollup scenario, where Alice submitted an assertion on Ethereum, but because the transaction data was unavailable, the OPR participants were unable to recalculate or challenge the assertion.
In order to cope with the above situation, the designs of both OPR and ZKR require operators to submit all transaction details to Ethereum as calldata. While this allows them to avoid DA issues in the short term, as the number of transactions within a rollup increases, the amount of data that needs to be committed also grows, limiting the amount of scaling these rollups can provide.
Even worse, data unavailability is an error that cannot be uniquely attributed. This means that participants cannot prove to other nodes that a specific block of data is missing. This is because Bob can broadcast that the block submitted by Alice is missing data, but when Charlie queries Alice, she may provide him with the data.
How do data availability issues affect current blockchains?
To answer this question, let’s first review the general block structure of an Ethereum-like blockchain, and the types of clients that exist on any blockchain network.
A block can be divided into two main parts:
Block header: A small block header contains summary and metadata related to the transactions included in the block.
Block body: contains all transaction data and constitutes the main part of the block.
In traditional blockchain protocols, all nodes are considered full nodes, they synchronize entire blocks and verify all state transitions. They require significant resources to check the validity of transactions and store blocks. The advantage is that these nodes will not accept any invalid transactions.
There may be another category of nodes that dont have (or dont want to spend) the resources to verify every transaction. Instead, they are primarily interested in understanding the current state of the blockchain and whether some transactions related to them are included in the chain. Ideally, these light clients should also be protected from being spoofed by chains containing invalid transactions. This can actually be achieved using so-called fraud proofs. These concise messages show that a specific block body contains invalid transactions. Any full node can generate such a fraud proof, so light clients do not have to trust a specific full node to be honest. They just need to make sure they are well connected to a gossip network that ensures that if a fraud proof of a block header is available, they will receive it.
However, there is a problem with this system: What if a block producer does not reveal the full data behind a block? In this case, full nodes will obviously reject the block because in their view, if a block does not come with a block body, then it is not even a block. However, light clients can be shown the block header chain and fail to notice missing data. At the same time, full nodes cannot produce fraud proofs because they lack the data required to create fraud proofs.
To deal with this problem, we need a mechanism for light clients to verify data availability. This will ensure that block producers hiding data cannot evade by convincing light clients. This would also force block producers to reveal partial data, allowing the entire network to access the entire block’s data in a collaborative manner.
Let’s understand this issue more deeply with an example. Suppose the block producer Alice constructs a block B containing transactions tx 1, tx 2, ..., txn. Assume that tx 1 is a malicious transaction. If tx 1 is broadcast, any full node can verify that it is malicious and send this information as a fraud proof to the light client, which will immediately know that the block is unacceptable. However, if Alice wants to hide tx 1 , she only reveals the header and all transaction data except tx 1 . A full node cannot verify the correctness of tx 1.
One might think that a simple solution would be to have all light clients randomly sample transactions, and if they find that their sample is available, they can be confident that the block is available. But if the light node randomly queries any transaction, the probability of the light client querying tx 1 is 1/n. Therefore, Alice can almost always trick a light client into accepting a malicious transaction. In other words, most light clients will be spoofed. Due to the non-attributable nature, a full node cannot prove in any way that tx 1 is unavailable. Unfortunately, increasing the sample size doesnt make things better either.
So, how do we solve this problem?
The solution to this problem lies in introducing redundancy in the blocks. There is a rich literature on coding theory, and erasure coding in particular, that can help us address this issue.
In short, erasure coding allows us to expand any n data blocks into 2n data blocks, such that any n of 2n are enough to reconstruct the original data (the parameters are adjustable, but here we keep it simple And consider this situation).
If we force block producers to erase-code transactions tx 1, tx 2, ..., txn, then to hide a single transaction it would need to hide n+ 1 data blocks, since any n data blocks are enough to build the entire transaction set. In this case, a small number of queries can give the light client a high degree of confidence that the underlying data is indeed available.
Woah,So thats it?
No. Although this simple trick makes it harder to hide data, it is still possible that the block producer deliberately went about erasure coding in the wrong way. However, a full node can verify that this erasure coding is done correctly, and if not, it can prove this to the light client. This is another type of proof of fraud, just like the malicious transaction mentioned above. Interestingly, all it takes is one honest full node as a neighbor of the light client to ensure that if a block is malicious, it will receive a fraud proof. This ensures that light clients can access a chain free of malicious transactions with a very high probability.
But theres a problem. If done too simply, some fraud proofs could be as large as the size of the block itself. Our resource assumptions about light clients prohibit us from using such a design. Improvements have been made through the use of multidimensional erasure coding techniques that reduce the size of fraud proofs at the cost of increasing the size of the commitment. For the sake of brevity, we do not go into detail about these here, but this articlepaperThis was analyzed in detail.
The problem with solutions based on fraud proofs is that a light client can never be completely certain of any block for which it has not yet received a fraud proof. At the same time, they continue to trust their full nodes to be honest. Honest nodes also need to be incentivized to continuously review blocks.
What we focus on here are those systems that guarantee that if a block encoding is invalid, full nodes can detect it and provide proof to light clients to convince them of misbehavior. However, in the next section, we will focus on block encodings that guarantee that only valid encodings are submitted to the chain. This eliminates the need for fraud proofs proving coding errors. Solutions based on validity proofs enable applications to use the system without having to wait for full nodes to provide such proofs of fraud.
So, how do these solutions work?
Recently, polynomial commitments have generated renewed interest in the blockchain space. These polynomial commitments, especially constant-size KZG/Kate commitments to polynomials, can be used to design a neat Data Availability (DA) scheme that does not require fraud proofs. In short, KZG commitment allows us to commit to a polynomial using a single elliptic curve group element. Furthermore, this scheme allows us to prove that at some point i, the polynomial φ has the value φ(i), using witnesses of constant size. This commitment scheme is computationally binding and also homomorphic, allowing us to neatly avoid fraud proofs.
We force the block producer to arrange the raw transaction data into a two-dimensional matrix of size nxm. It uses polynomial interpolation to expand each column of size n to a column of size 2 n . Each row of this expansion matrix generates a polynomial commitment and these commitments are sent as part of the block header. A schematic representation of the blocks is given below.
The light client queries any cell of this extended matrix for a proof, which allows it to immediately verify against the block header. Constant size proofs of membership make sampling extremely efficient. The homomorphic nature of commitments ensures that proofs can only be verified if the block is constructed correctly, while polynomial interpolation ensures that a constant number of successful samples means the probability of data availability is very high.
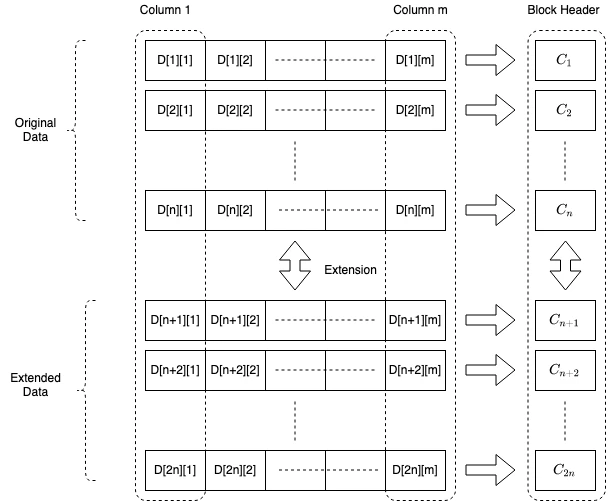
Schematic representation of blocks
The finer details of this scheme, as well as further optimization and cost estimation, are beyond the scope of this article. However, we would like to point out that although we are discussing a two-dimensional scheme here, similar guarantees can also be provided by a one-dimensional scheme, which has a smaller block header size, but at the cost of reduced parallelism and light client sampling efficiency. We will explore this in more depth in a subsequent article.
What are the other alternatives? What happens next?
High-dimensional erasure coding and KZG commitments are not the only solutions to data availability problems. We have omitted here some other methods, such as coded Merkle trees, coded interleaved trees, FRI, and STARK-based methods, but each method has its advantages and disadvantages.
At Avail, we have been developing data availability solutions using the KZG Commitment. In subsequent articles, we will cover implementation details, how to use it, and how we plan to change the data availability problem space. To learn more about Avail, follow us on Twitter and join our Discord server.
Twitter:https://twitter.com/AvailProject
Discord:https://discord.com/invite/jTkvDrZ54r
You are also welcome to follow Modular 101’s Twitter account: @Modular 101










