What is FHE
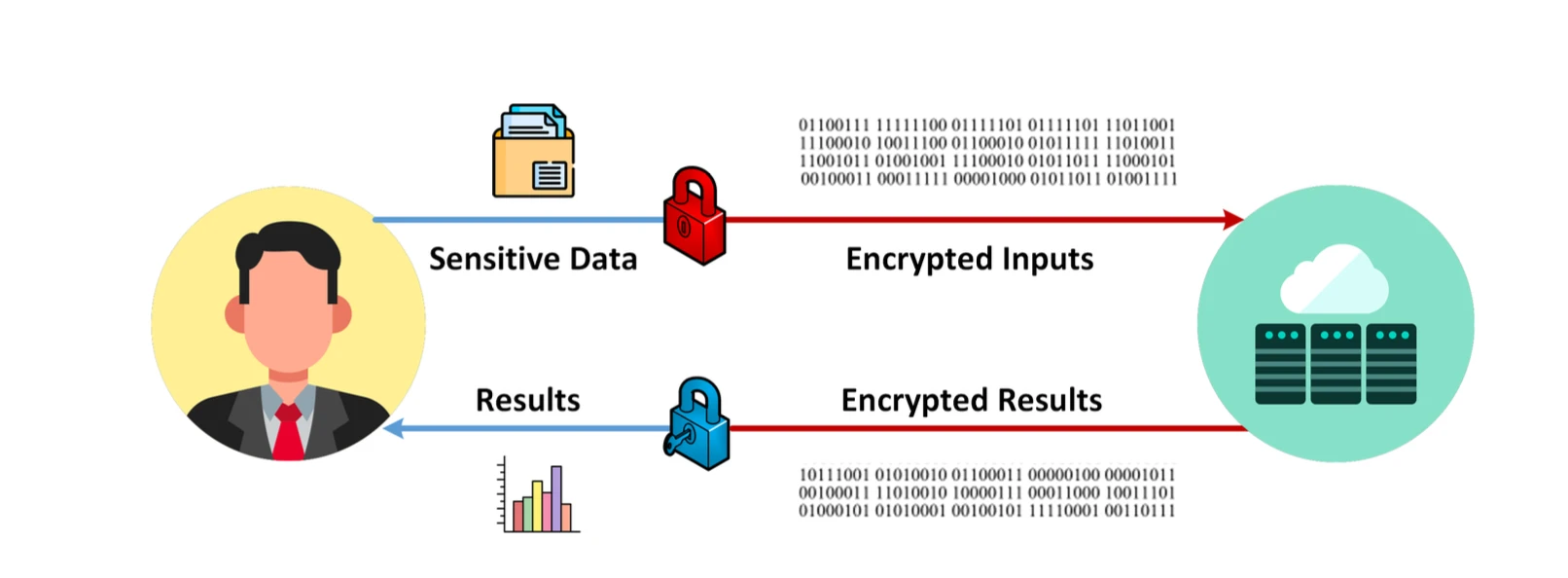
FHE process, source: Data Privacy Made Easy
FHE (Fully homomorphic encryption) is an advanced encryption technology that supports direct computation on encrypted data. This means that data can be processed while protecting privacy. FHE has multiple application scenarios, especially in data processing and analysis under privacy protection, such as finance, healthcare, cloud computing, machine learning, voting systems, the Internet of Things, blockchain privacy protection and other fields. However, commercialization still requires some time. The main problem is that the computational and memory overhead brought by its algorithm is extremely large, and the scalability is poor. Next, we will briefly walk through the basic principles of the entire algorithm and focus on the problems faced by this cryptographic algorithm.
Rationale
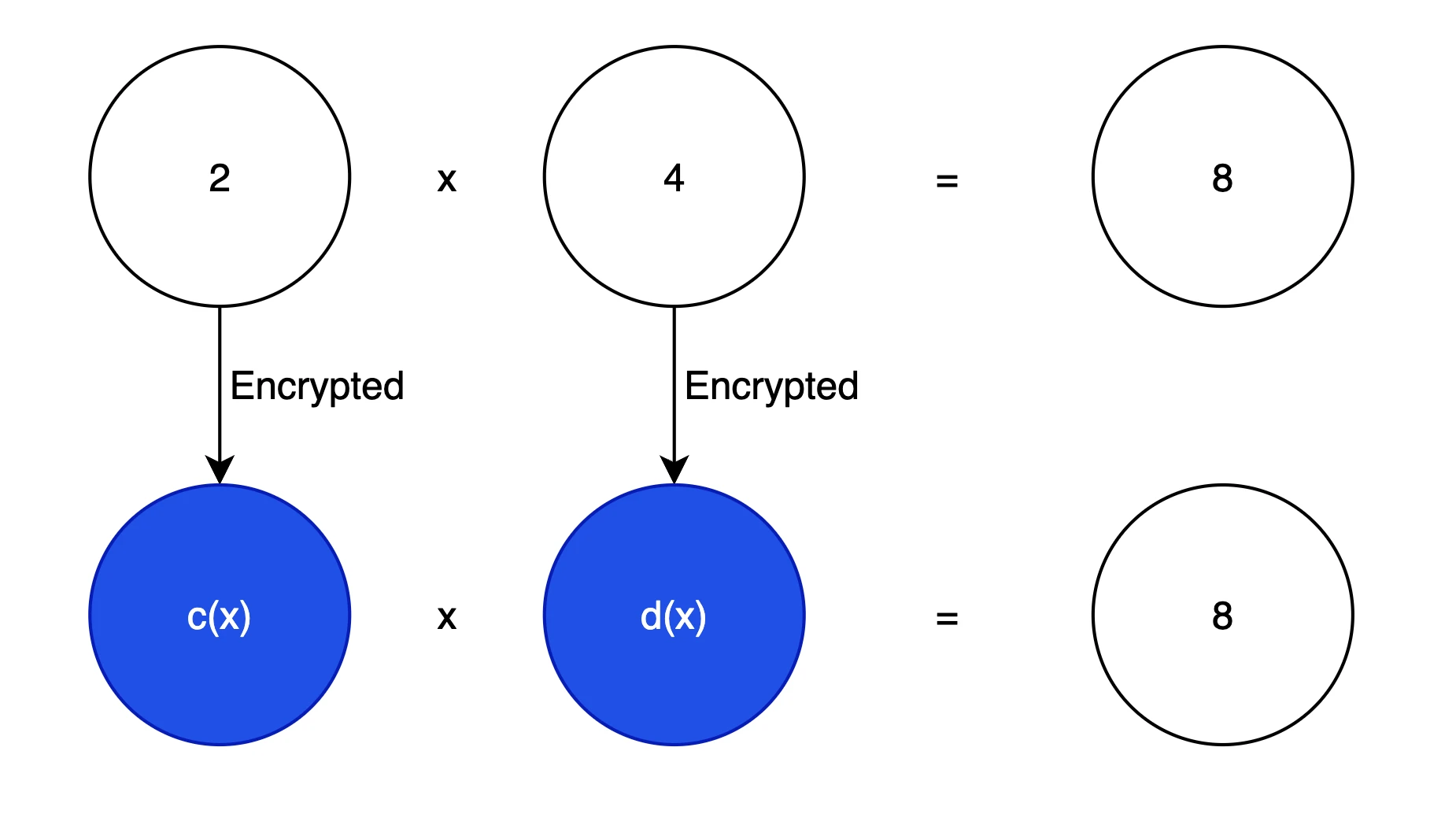
Homomorphic encryption diagram
First, we need to perform calculations on encrypted data and still get the same result, as shown in the visualization above. This is our basic goal. In cryptography, polynomials are often used to hide the original information, because polynomials can be converted into linear algebra problems or vector calculation problems, which makes it easier for modern computers that are highly optimized for vectors to perform operations (such as parallel computing). For example, 3 x 2 + 2 x + 1 can be represented as a vector [ 1, 2, 3 ].
Suppose, we want to encrypt 2, in a simplified HE system, we might:
Choose a key polynomial, such as s(x) = 3 x 2 + 2 x + 1
Generate a random polynomial, such as a(x) = 2 x 2 + 5 x + 3
Generate a small wrong polynomial, such as e(x) = -1 x + 2
Encryption 2 -> c(x) = 2 + a(x)*s(x) + e(x)
Lets talk about why we need to do this. Now assume that we have the ciphertext c(x). If we want to get the plaintext m, the formula is c(x) - e(x) - a(x)*s(x) = 2. Here, our random polynomial assumes that a(x) is public. Then we just need to ensure that our key s(x) is kept confidential. If we know s(x), and add c(x) as a very small error, then theoretically it can be ignored and we can get the plaintext m.
Here comes the first question. There are so many polynomials. How to choose a polynomial? What is the best degree of a polynomial? In fact, the degree of a polynomial is determined by the algorithm that implements HE. It is usually a power of 2, such as 1024/2048. The coefficients of the polynomial are randomly selected from a finite field q. For example, mod 10000, it is randomly selected from 0-9999. There are many algorithms to follow for random selection of coefficients, such as uniform distribution, discrete Gaussian distribution, etc. Different schemes also have different coefficient selection requirements, usually to meet the principle of fast solution under the scheme.
The second question is, what is noise? Noise is used to confuse attackers, because if all our numbers are s(x) and the random polynomial is in a domain, then there is a certain pattern. As long as the plaintext m is input enough times, the information of s(x) and c(x) can be determined based on the output c(x). If the noise e(x) is introduced, it can be guaranteed that s(x) and c(x) cannot be obtained by simple repeated enumeration, because there is a completely random small error. This parameter is also called the noise budget. Assuming q = 2 ^ 32, the initial noise may be around 2 ^ 3. After some operations, the noise may grow to 2 ^ 20. At this time, there is still enough space for decryption, because 2 ^ 20 << 2 ^ 32.
After we obtain the polynomial, we now need to convert the c(x) * d(x) operation into a circuit, which often appears in ZKP, mainly because the abstract concept of circuit provides a universal computing model to represent any calculation, and the circuit model allows accurate tracking and management of the noise introduced by each operation, and is also convenient for subsequent introduction into professional hardware such as ASIC and FPGA for accelerated computing, such as the SIMD model. Any complex operation can be mapped into simple modular circuit elements, such as addition and multiplication.

Arithmetic Circuit Representation
Addition and multiplication can express subtraction and division, and therefore any calculation. The coefficients of the polynomial are expressed in binary and are called the inputs of the circuit. Each node of the circuit represents an addition or multiplication. Each (*) represents a multiplication gate, and each (+) represents an addition gate. This is the algorithmic circuit.
This leads to a problem. In order to prevent the leakage of semantic information, we introduced e(x), which is called noise. In our calculation, addition will turn two e(x) polynomials into polynomials of the same degree. In multiplication, multiplying two noise polynomials will increase the degree of e(x) and the size of the text exponentially. If the noise is too large, the noise cannot be ignored during the calculation of the result, and the original text m cannot be restored. This is the main reason that limits the HE algorithm to express arbitrary calculations, because the noise will grow exponentially and quickly reach the unusable threshold. In the circuit, this is called the depth of the circuit, and the number of multiplication operations is the depth value of the circuit.
The basic principle of homomorphic encryption (HE) is shown in the figure above. In order to solve the noise problem that restricts homomorphic encryption, several solutions have been proposed:
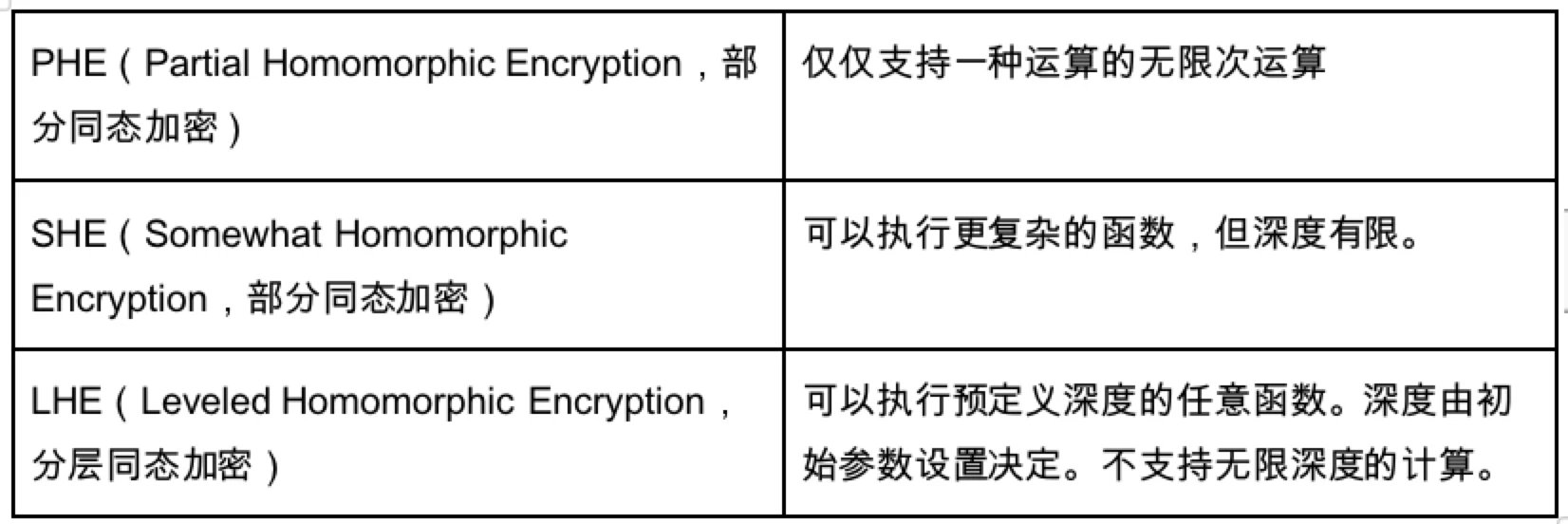
LHE is a very suitable algorithm here, because under this algorithm, as long as the depth is determined, any function can be executed within the depth, but PHE and SHE cannot achieve Turing completeness. Therefore, based on this, cryptographers conducted research and proposed three technologies to build FHE fully homomorphic encryption, hoping to realize the vision of executing any function at infinite depth.
Key switching: After multiplication, the size of the ciphertext will grow exponentially, which will place great demands on the memory and computing resources of subsequent operations. Therefore, implementing key switching after each multiplication can compress the ciphertext, but it will introduce a little noise.
Modulus Switching: Both multiplication and key switching will increase the noise exponentially. The modulus q is the Mod 10000 we mentioned earlier. It can only take parameters in [0, 9999]. The larger the q, the more likely it is that the noise will still be within q after multiple calculations, and decryption is possible. Therefore, after multiple operations, in order to avoid the exponential increase of noise exceeding the threshold, Modulus Switching is needed to reduce the noise budget, so that the noise can be suppressed. Here we can get a basic principle. If our calculation is very complex and the circuit depth is very large, then a larger modulus q noise budget is needed to accommodate the availability after multiple exponential increases.
Bootstrap: However, if you want to achieve infinite depth calculation, Modulus can only limit the growth of noise, but each switch will make the q range smaller. We know that once it is reduced, it means that the complexity of the calculation needs to be reduced. Bootstrap is a refresh technology, which resets the noise to the original level instead of reducing the noise. Bootstrap does not need to reduce the modulus, so it can maintain the computing power of the system. But its disadvantage is that it consumes a lot of computing resources.
In general, for calculations under finite steps, using Modulus Switching can reduce noise, but it will also reduce the modulus, that is, the noise budget, resulting in compressed computing power. Therefore, this is only for calculations under finite steps. For Bootstrap, noise reset can be achieved, so based on the LHE algorithm, true FHE can be achieved, that is, infinite calculation of any function, and this is also the meaning of Fully FHE.
However, the disadvantage is that it consumes a lot of computing resources. Therefore, in general, these two noise reduction technologies are used in combination. Modulus switching is used for daily noise management, and the delay requires bootstrap time. When modulus switching cannot further effectively control the noise, bootstrap with higher computing cost is used.
Currently, the FHE solution has the following specific implementations, all of which use the Bootstrap core technology:
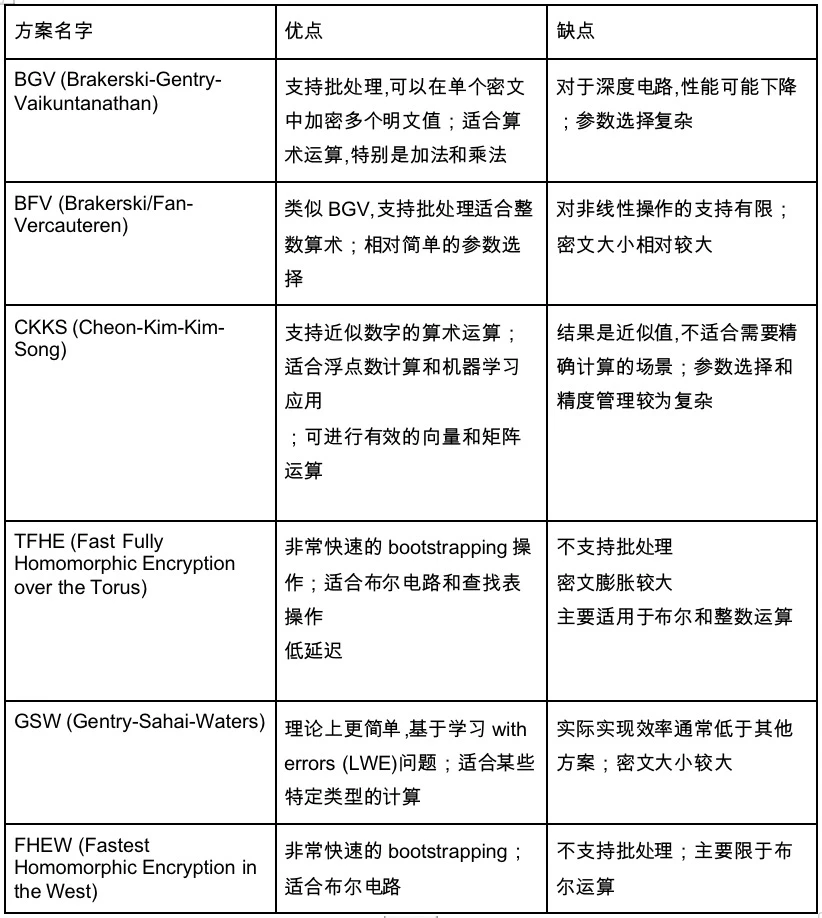
This brings us to the circuit type we have not discussed so far. We mainly introduced arithmetic circuits above. But there is another type of circuit - Boolean circuit. Arithmetic circuits are more abstract, such as 1+1, and the nodes are also addition or division, while all numbers in Boolean circuits are converted to 01 base, and all nodes are bool operations, including NOT, OR, and AND operations, similar to the circuit implementation of our computers. Arithmetic circuits are more abstract circuits.
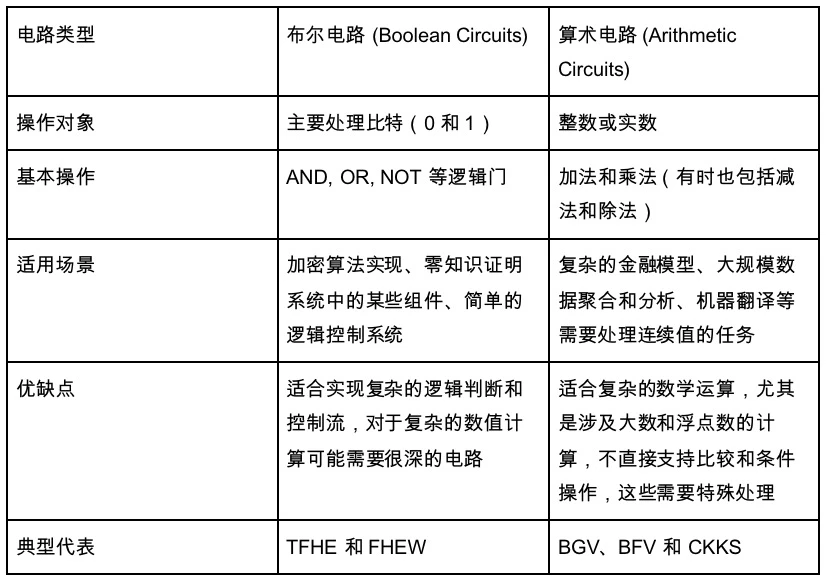
Therefore, we can very roughly think of Boolean operations as flexible processing that is not so data-intensive, while arithmetic operations are solutions for data-intensive applications.
Problems with FHE
Since our calculation needs to be encrypted and then converted into a circuit, and since the pure calculation only calculates 2+4, but after encryption, a large number of cryptographic indirect calculation processes are introduced, as well as some cutting-edge technologies such as Bootstrap to solve the noise problem, which results in its computational overhead being N orders of magnitude of ordinary calculations.
Lets use a real-world example to give readers a sense of the computing resource overhead of these additional cryptographic processes. Assuming that ordinary calculations require 200 clock cycles on a 3 GHz processor, then an ordinary AES-128 decryption takes about 67 nanoseconds (200/3 GHz). The FHE version takes 35 seconds, which is about 522,388,060 times (35/67 e-9) the ordinary version. In other words, using the same computing resources, the same ordinary algorithm and the algorithm under FHE calculation require about 500 million times more computing resources.

DARPA dprive program, source: DARPA
For data security, the US DARPA specially built a Dprive program in 2021 and invited multiple research teams including Microsoft and Intel. Their goal is to create an FHE accelerator and a supporting software stack to make the FHE computing speed more consistent with similar operations on unencrypted data, and achieve the goal of FHE computing speed being about 1/10 of ordinary computing. Tom Rondeau, DARPA project manager, pointed out: It is estimated that in the FHE world, our computing speed is about a million times slower than in the plain text world.
Dprive mainly focuses on the following aspects:
Increase the word length of the processor: Modern computer systems use a word length of 64 bits, which means that a number is at most 64 bits, but in reality q is often 1024 bits. If we want to achieve this, we have to split our q, which will consume memory resources and speed. Therefore, in order to achieve a larger q, we need to build a processor with a word length of 1024 bits or larger. The finite field q is very important. As we mentioned earlier, the larger it is, the more computable steps there are, and the bootstrap operation can be postponed as much as possible, so that the overall computing resource consumption will be reduced. q plays a core role in FHE. It affects almost all aspects of the scheme, including security, performance, the amount of computation that can be performed, and the memory resources required.
Build an ASIC processor: We mentioned earlier that due to the convenience of parallelization and other reasons, we built polynomials and constructed circuits through polynomials, which is similar to ZK. Current CPUs and GPUs do not have the ability (computing resources and memory resources) to run circuits, and special ASIC processors need to be built to allow FHE algorithms.
Building a parallel architecture MIMD. Unlike the SIMD parallel architecture, SIMD can only execute a single instruction on multiple data, that is, data splitting and parallel processing, but MIMD can split data and use different instructions for calculation. SIMD is mainly used for data parallelism, which is also the main architecture for parallel transaction processing in most blockchain projects. MIMD can handle various types of parallel tasks. MIMD is more technically complex and needs to focus on synchronization and communication issues.
There is only one month left before DARPAs DEPRIVE program expires. Originally, DPRIVE was planned to start in 2021 and end in three phases in September 2024, but its progress seems to be slow and it has not yet achieved the expected goal of 1/10 efficiency compared to ordinary computing.
Although the progress of breaking FHE technology is slow, similar to ZK technology, it faces the serious problem that hardware landing is the prerequisite for technology landing. However, we still believe that in the long run, FHE technology still has its unique significance, especially in protecting the privacy of some security data listed in the first part. For the DARPA Department of Defense, it has a lot of sensitive data. If it wants to release AI generic capabilities to the military, it needs to train AI in the form of data security. Not only that, it also applies to key sensitive data such as medical and financial. In fact, FHE is not suitable for all ordinary calculations, but is more oriented to the computing needs under sensitive data. This security is particularly important in the post-quantum era.
For this cutting-edge technology, we must consider the time difference between the investment cycle and commercialization. Therefore, we need to be very cautious about the landing time of FHE.
Integration of blockchain
In blockchain, FHE is also mainly used to protect the privacy of data. Its application areas include on-chain privacy, privacy of AI training data, on-chain voting privacy, and on-chain privacy transaction review. FHE is also known as one of the potential solutions for the on-chain MEV solution. According to our MEV article Illuminating the Dark Forest - Unveiling the Mystery of MEV , many current MEV solutions are just ways to rebuild the MEV architecture, not solutions. In fact, the UX problem caused by the sandwich attack has not been solved. The solution we thought of at the beginning was to directly encrypt the transaction while keeping the status public.
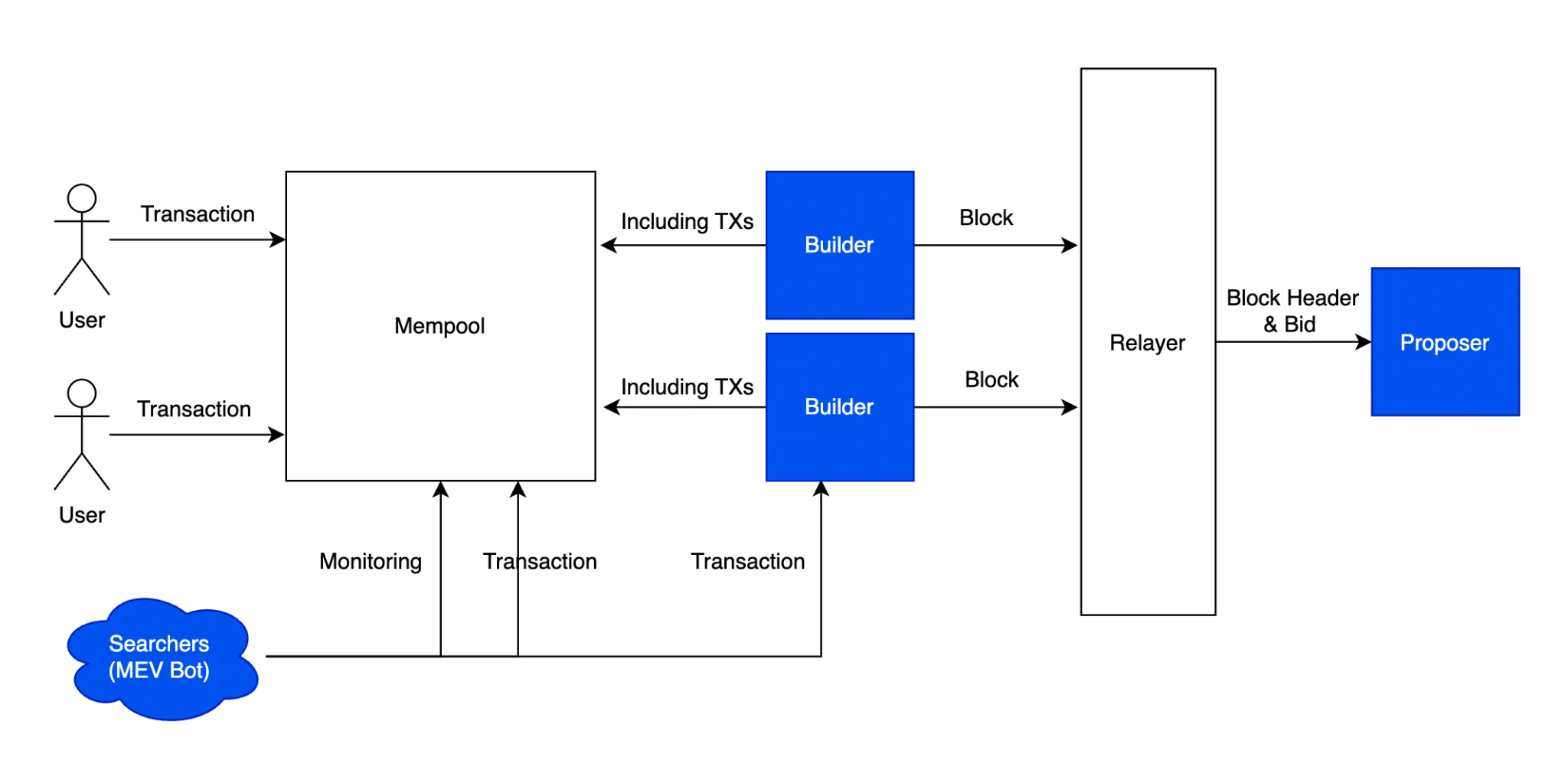
MEV PBS Procedure
But there is also a problem. If we completely encrypt the transactions, the positive externalities brought by MEV bots will also disappear. The validator Builder needs to run FHE based on the virtual machine, and the validator also needs to verify the transaction to determine the correctness of the final state. This will significantly increase the requirements for running nodes and slow down the throughput of the entire network by a million times.
Main Projects
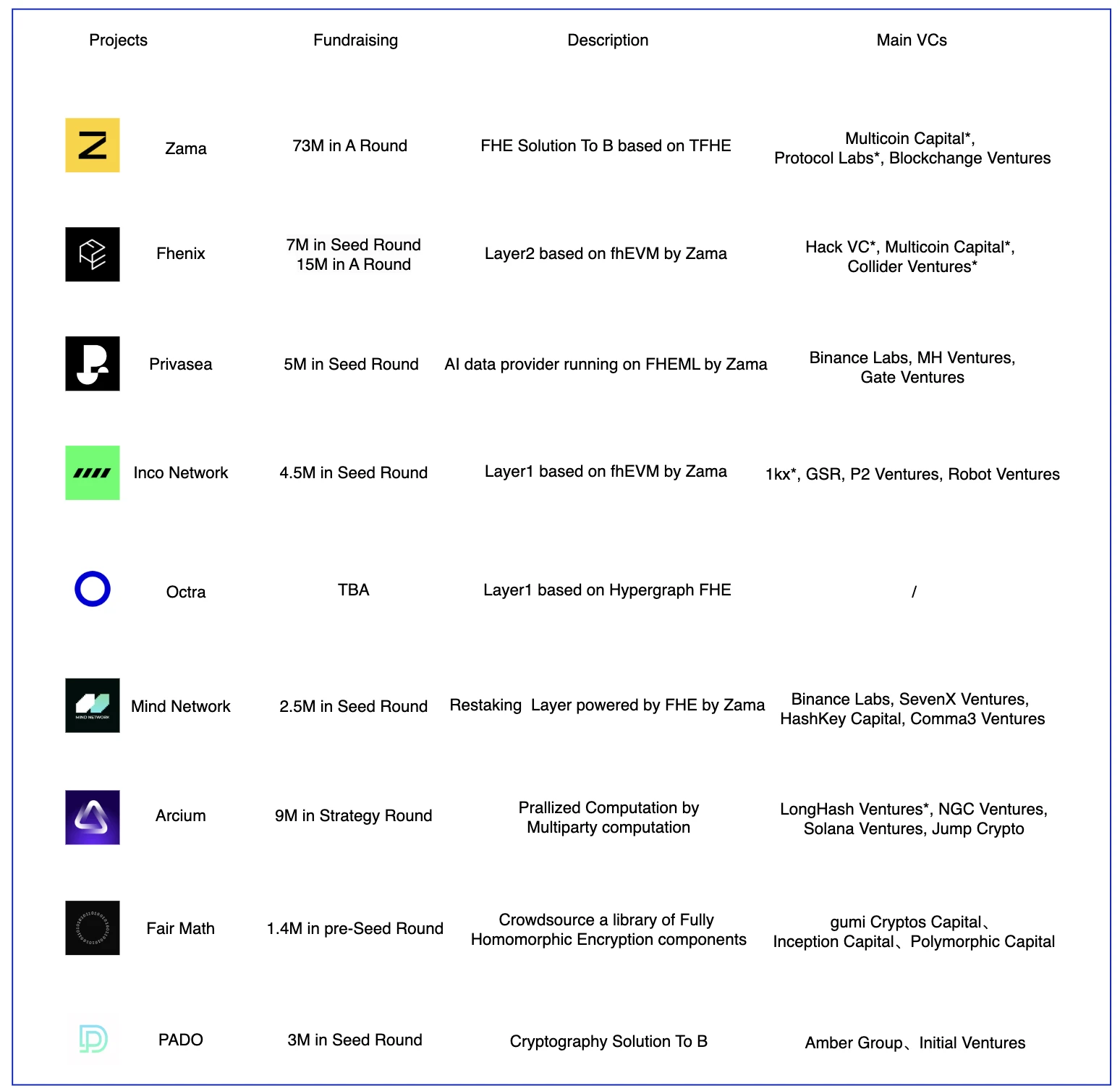
FHE Landscape
FHE is a relatively new technology. Currently, most projects use FHE technology built by Zama, such as Fhenix, Privasea, Inco Network, and Mind Network. Zamas FHE engineering implementation capabilities have been recognized by these projects. Most of the above projects are built based on the libraries provided by Zama, and the main difference lies in the business model. Fhenix hopes to build a privacy-first Optimism Layer 2, and Privasea hopes to use the capabilities of FHE to perform LLM data operations, but this is a very data-heavy operation, and the technical and hardware requirements for FHE are particularly high. Then Zamas TFHE may not be the best choice. Inco Network and Fhenix both use fhEVM, but one is to build Layer 1 and the other is Layer 2. Arcium has built a fusion of multiple cryptographic technologies, including FHE, MPC, and ZK. Mind Networks business model is relatively unconventional. It chose the Restaking track and solved the problems of economic security and voting trust at the consensus layer by providing liquid security and a subnet architecture based on FHE.
Zama
Zama is a solution based on TFHE, which features the use of Bootstrap technology and focuses on processing Boolean operations and low-word-length integer operations. Although it is a faster technical implementation in our implementation of FHE, it is still far behind ordinary computing. Secondly, it cannot implement arbitrary computing. When facing data-intensive tasks, these operations will cause the circuit depth to be too large to handle. It is not a data-intensive solution and is only suitable for encryption processing of certain key steps.
TFHE currently has ready-made implementation code. Zamas main work is to rewrite TFHE in Rust, which is its rs-TFHE crates. At the same time, in order to lower the threshold for users to use Rust, it also built a transpilation tool Concrate, which can convert Python into rs-TFHE equivalent. Using this tool, you can translate large model languages based on Python into rust language based on TFHE-rs. In this way, large models based on homomorphic encryption can be run, but data-intensive tasks at this time are not actually suitable for TFHE scenarios. Zamas product fhEVM is a technology that uses fully homomorphic encryption (FHE) to implement confidential smart contracts on EVM, which can support end-to-end encrypted smart contracts compiled based on Solidity language.
In general, as a To B product, Zama has built a relatively complete blockchain + AI development stack based on TFHE, which can help web3 projects to easily build FHE infrastructure and applications.
Octra
What is special about Octra is that it uses a different technology to implement FHE. It uses a technology called hypergraphs to implement bootstrap. It is also based on Boolean circuits, but Octra believes that hypergraphs-based technology can achieve more efficient FHE. This is Octras original technology for implementing FHE, and the team has very strong engineering and cryptography capabilities.
Octra built a new smart contract language, which is developed using code libraries such as OCaml, AST, ReasonML (a language specifically for smart contracts and applications that interact with the Octra blockchain network), and C++. The Hyperghraph FHE library it built is compatible with any project.
Its architecture is similar to projects such as Mind Network, Bittensor, and Allora. It builds a main network, and then other projects become subnets, building an isolated operating environment. At the same time, similar to these projects, they all build emerging consensus protocols that are more suitable for the architecture itself. Octra builds a machine learning-based consensus protocol ML-consensus, which is essentially based on DAG (directed acyclic graph).
The technical principle of this consensus has not been disclosed yet, but we can roughly speculate. The transaction is submitted to the network, and then the SVM (support vector machine) algorithm is used to determine the best processing node, mainly based on the current network load of each node. The system will determine the best parent node consensus path based on historical data (ML algorithm learning). As long as 1/2 of the nodes are satisfied, the consensus of the growing database can be reached.
expect
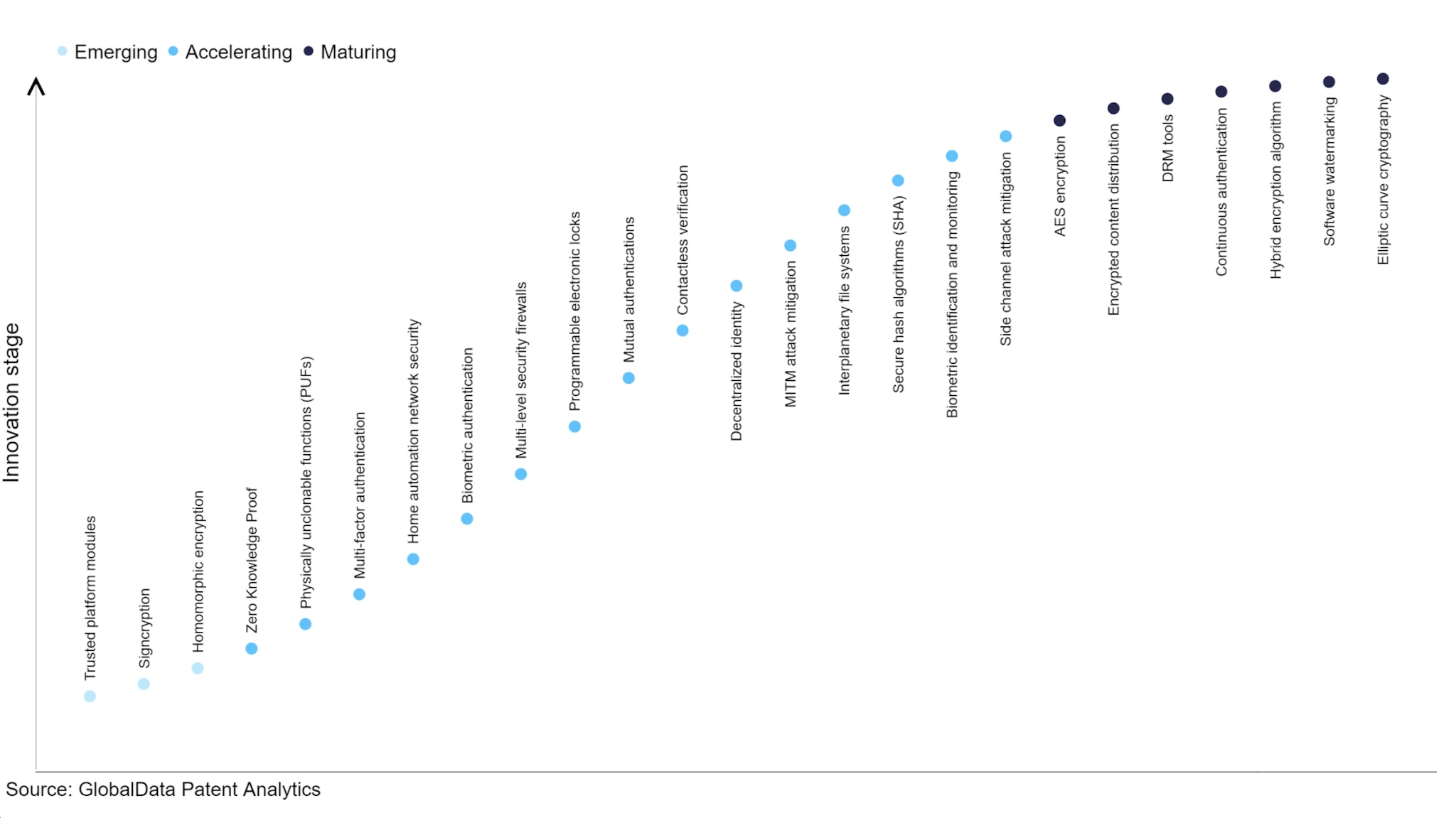
Current status of cutting-edge cryptography technology development, source: Verdict
FHE technology is a future-oriented technology, and its development status is still not as good as ZK technology. There is a lack of capital investment, because the inefficiency and high cost brought by privacy protection are not enough motivation for most commercial organizations. The development of ZK technology has become faster because of the investment of Crypto VC. FHE is still in its very early stages. Even now, there are still few projects on the market because of its high cost, high engineering difficulty, and unclear prospects for commercialization. In 2021, DAPRA joined forces with many companies such as Intel and Microsoft to launch a 42-month FHE attack plan. Although some progress has been made, it is still far from the performance target. With the attention of Crypto VC to this direction, more funds will flow into this industry. It is expected that more FHE projects will appear in the industry, and more teams with strong engineering and research capabilities such as Zama and Octra will stand in the center of the stage. The combination of FHE technology with the commercialization and development status of blockchain is still worth exploring. At present, the best application is the anonymization of verification node voting, but the scope of application is still narrow.
Like ZK, the implementation of FHE chips is one of the prerequisites for the commercialization of FHE. Currently, many manufacturers such as Intel, Chain Reaction, and Optalysys are exploring this aspect. Even though FHE faces many technical obstacles, with the implementation of FHE chips, fully homomorphic encryption, as a technology with great prospects and definite needs, will bring profound changes to industries such as defense, finance, and medical care, and release the potential of combining these privacy data with future technologies such as quantum algorithms, and will also usher in its explosive moment.
We are willing to explore this early frontier technology. If you are building a truly commercial FHE product, or have more cutting-edge technological innovations, please contact us!










