FHE 란 무엇입니까?
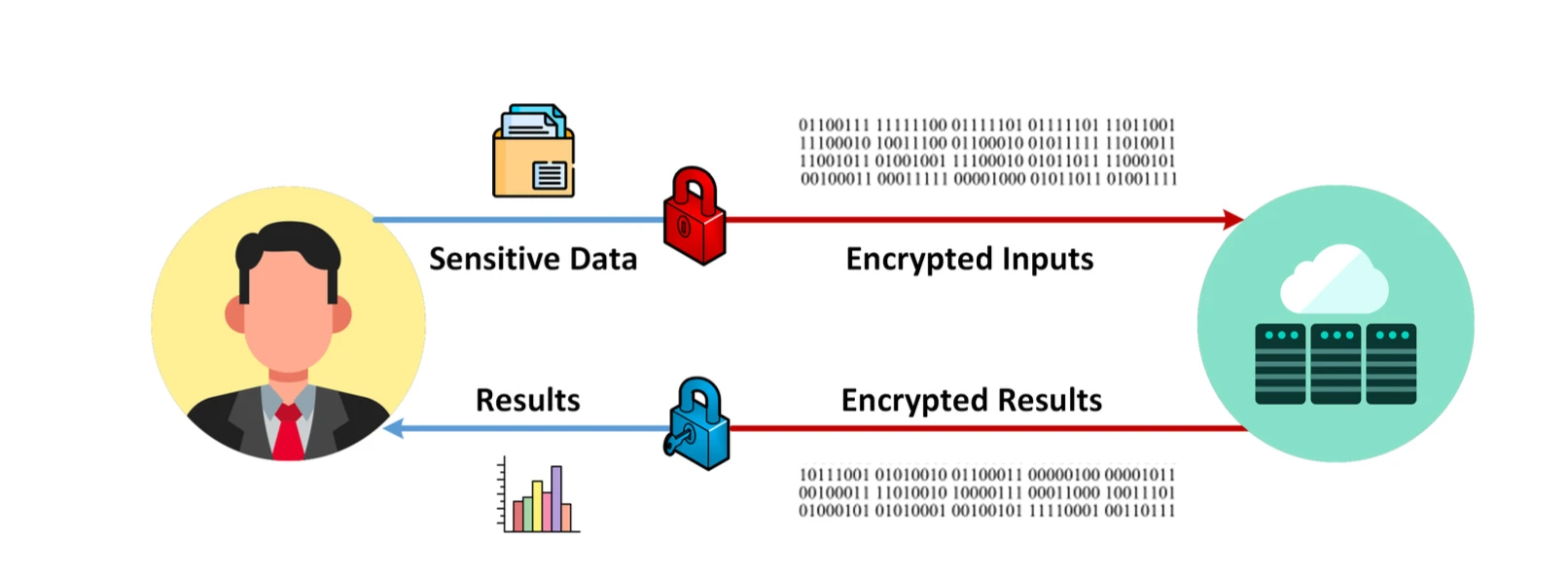
FHE 프로세스, 이미지 출처: 데이터 개인정보 보호가 쉬워졌습니다.
FHE(Fully Homomorphic Encryption)는 암호화된 데이터에 대한 직접 계산을 지원하는 고급 암호화 기술입니다. 이는 개인 정보를 보호하면서 데이터를 처리할 수 있음을 의미합니다. FHE에는 특히 금융, 의료 건강, 클라우드 컴퓨팅, 기계 학습, 투표 시스템, 사물 인터넷, 블록체인 개인 정보 보호 및 기타 분야와 같은 개인 정보 보호 하의 데이터 처리 및 분석과 같은 적용 가능한 시나리오가 많이 있습니다. 그러나 상용화에는 여전히 일정 시간이 걸린다. 가장 큰 문제는 알고리즘으로 인해 발생하는 계산 및 메모리 오버헤드가 매우 크고 확장성이 좋지 않다는 점이다. 다음으로 전체 알고리즘의 기본 원리를 간략하게 살펴보고 이 암호화 알고리즘이 직면한 문제에 중점을 둘 것입니다.
기본 원리
동형 암호화 아이콘
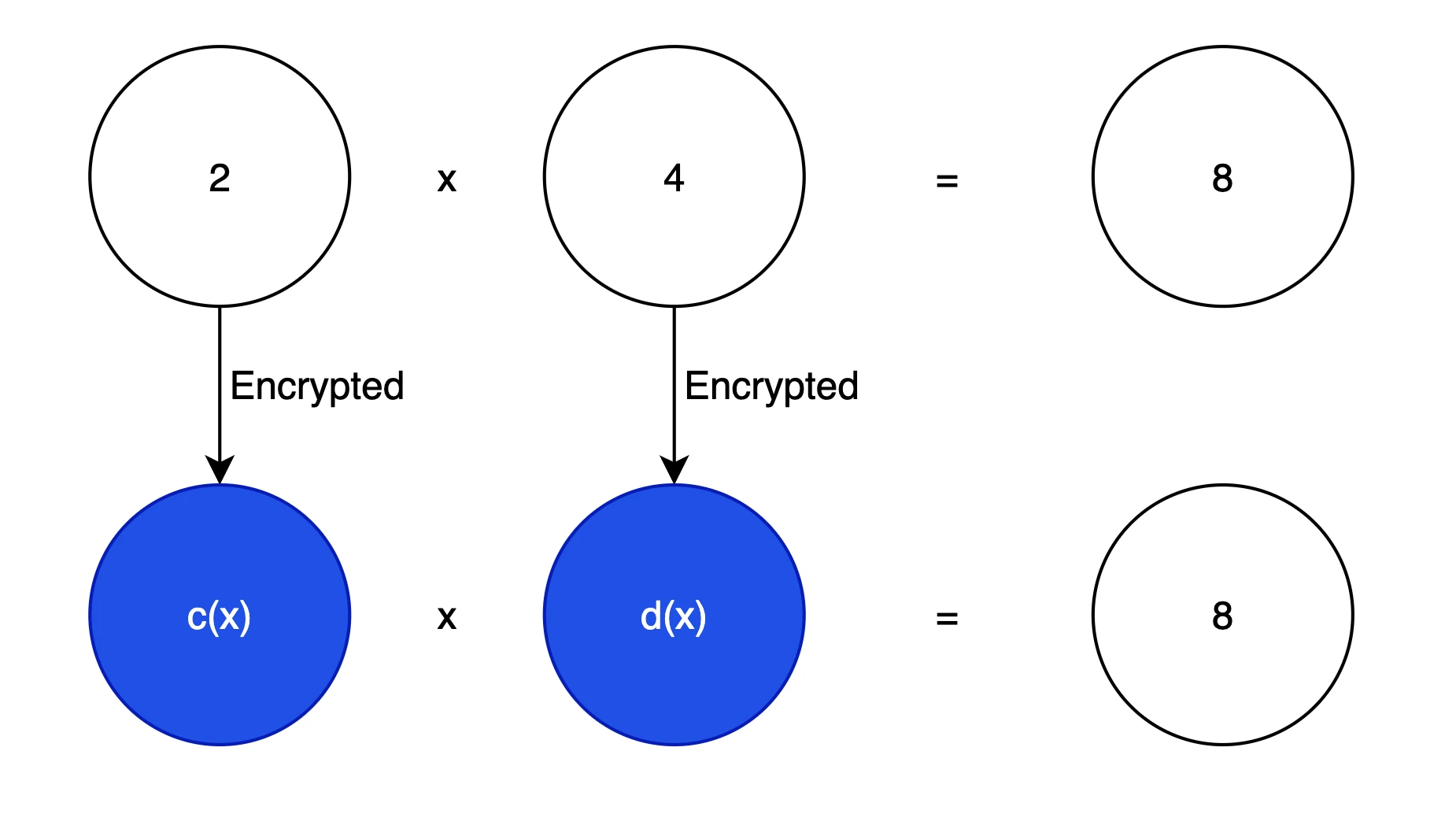
먼저, 암호화된 데이터에 대해 계산을 수행하고 위 그림과 같이 시각화한 동일한 결과를 얻어야 합니다. 이것이 우리의 기본 목표입니다. 암호화에서 다항식은 일반적으로 원본 텍스트의 정보를 숨기기 위해 사용됩니다. 다항식은 선형 대수 문제로 변환될 수 있고 벡터 계산 문제로도 변환될 수 있기 때문에 벡터에 고도로 최적화된 최신 컴퓨터가 연산을 수행하는 데 도움이 됩니다(예: 병렬 컴퓨팅) ), 예를 들어 3 x 2 + 2 x + 1은 벡터 [1, 2, 3]으로 표현될 수 있습니다.
단순화된 HE 시스템에서 2 를 암호화하려고 한다고 가정하면 다음과 같이 할 수 있습니다.
s(x) = 3 x 2 + 2 x + 1과 같은 키 다항식을 선택합니다.
a(x) = 2 x 2 + 5 x + 3과 같은 임의 다항식을 생성합니다.
e(x) = -1 x + 2와 같은 작은 잘못된 다항식을 생성합니다.
암호화 2 -> c(x) = 2 + a(x)*s(x) + e(x)
이제 암호문 c(x)를 얻었다고 가정해 보겠습니다. 일반 텍스트 m을 얻으려면 공식은 c(x) - e(x) - a(x)입니다. *s(x) = 2, 여기서 임의 다항식은 a(x)가 공개라고 가정하므로 s(x)와 c(x)를 알고 있는 경우에만 키 s(x)가 기밀인지 확인하면 됩니다. 오류가 매우 작은 경우 이론적으로 무시할 수 있으며 평문 m을 얻을 수 있습니다.
첫 번째 질문은 다음과 같습니다. 다항식이 너무 많습니다. 다항식을 선택하는 방법은 무엇입니까? 가장 좋은 다항식 차수는 무엇입니까? 실제로 다항식의 차수는 HE를 구현하는 데 사용되는 알고리즘에 의해 결정됩니다. 일반적으로 1024/2048 등과 같이 2의 거듭제곱입니다. 다항식의 계수는 mod 10000과 같은 유한 필드 q에서 무작위로 선택한 다음 0-9999에서 무작위로 선택됩니다. 균일 분포, 이산 가우스 분포 등과 같은 계수의 무작위 선택을 위한 많은 알고리즘이 있습니다. 또한 다양한 방식에는 일반적으로 해당 방식에서 빠른 솔루션 원칙을 충족하기 위해 서로 다른 계수 선택 요구 사항이 있습니다.
두 번째 질문, 소음이란 무엇입니까? 노이즈는 공격자를 혼란스럽게 하는 데 사용됩니다. 왜냐하면 모든 숫자가 s(x)이고 임의의 다항식이 도메인에 있다고 가정하면 출력에 따라 일반 텍스트 m이 충분히 입력되는 한 특정 규칙이 있기 때문입니다. c(x), 이 두 s(x)와 c(x)의 정보를 판단할 수 있습니다. 잡음 e(x)가 도입되면 완전히 무작위적인 작은 오류가 있기 때문에 단순 반복 열거를 통해 s(x)와 c(x)를 얻을 수 없다는 것이 보장됩니다. 이 매개변수는 소음 예산이라고도 합니다. q = 2^32라고 가정하면 초기 잡음은 약 2^3이 될 수 있습니다. 일부 작업 후에는 소음이 2^20까지 커질 수 있습니다. 2^20 << 2^32이므로 이 시점에서는 여전히 암호 해독을 위한 충분한 공간이 있습니다.
다항식을 얻은 후에는 이제 c(x) * d(x) 연산을 회로로 변환해야 합니다. 이는 주로 ZKP에 나타나는데, 주로 회로의 추상 개념이 모든 것을 나타내는 일반적인 컴퓨팅 모델을 제공하기 때문입니다. 계산 및 회로 모델을 통해 각 작업에서 발생하는 노이즈를 정확하게 추적 및 관리할 수 있으며, SIMD 모델과 같은 계산 가속화를 위해 ASIC 및 FPGA와 같은 전문 하드웨어에 대한 후속 도입도 용이하게 됩니다. 복잡한 연산은 덧셈, 곱셈과 같은 간단한 모듈식 회로 요소로 매핑될 수 있습니다.

산술 회로 표현
덧셈과 곱셈은 뺄셈과 나눗셈, 즉 모든 계산을 표현할 수 있습니다. 다항식의 계수는 이진수로 표시되며 회로에 대한 입력이라고 합니다. 각 회로 노드는 덧셈이나 곱셈의 실행을 나타냅니다. 각 (*)는 곱셈 게이트를 나타내고, 각 (+)는 덧셈 게이트를 나타냅니다. 이것이 알고리즘 회로이다.
이는 의미론적 정보를 유출하지 않기 위해 노이즈라고 불리는 e(x)를 도입합니다. 우리의 계산에서 덧셈은 두 개의 e(x) 다항식을 같은 차수의 다항식으로 바꿉니다. 곱셈에서는 두 개의 노이즈 다항식을 곱하면 e(x)의 정도와 텍스트의 크기가 기하급수적으로 증가합니다. 노이즈가 너무 크면 결과 계산 시 노이즈를 무시할 수 없으며 원본 텍스트는 m입니다. 복원할 수 없습니다. 이는 노이즈가 기하급수적으로 증가하여 사용할 수 없는 임계값에 빠르게 도달하기 때문에 임의의 계산을 표현하는 HE 알고리즘의 기능을 제한하는 주요 이유입니다. 회로에서는 이를 회로의 깊이라고 하며, 곱셈 연산의 횟수는 회로의 깊이 값이다.
동형암호 HE의 기본 원리는 위 그림에 나와 있습니다. 동형암호를 제한하는 잡음 문제를 해결하기 위해 여러 가지 솔루션이 제안되었습니다.
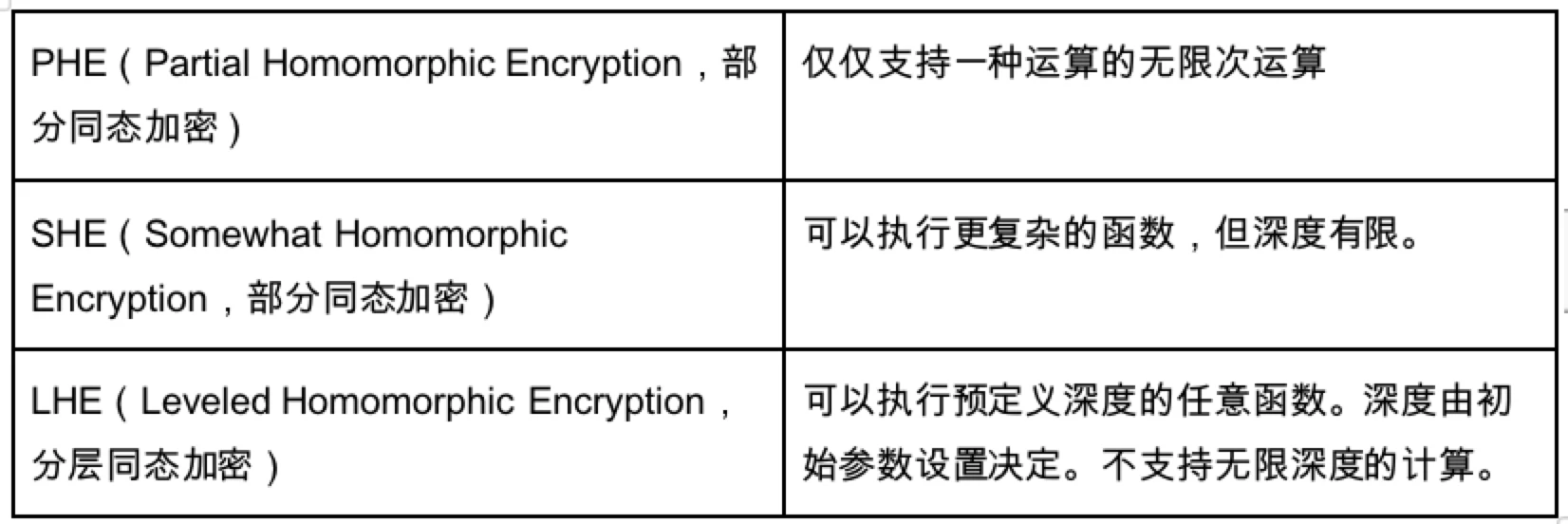
LHE는 여기서 매우 적합한 알고리즘입니다. 왜냐하면 이 알고리즘에서는 깊이가 결정되는 한 깊이 내에서 모든 기능을 실행할 수 있지만 PHE와 SHE는 튜링 완전성을 달성할 수 없기 때문입니다. 따라서 이를 바탕으로 암호학자들은 무한 깊이에서 임의의 기능을 실행한다는 비전을 실현하기 위해 연구를 수행하고 FHE 완전 동형 암호화를 구축하기 위한 세 가지 기술을 제안했습니다.
키 전환: 곱셈 후에 암호문의 크기는 기하급수적으로 증가하므로 후속 작업을 위한 메모리 및 컴퓨팅 리소스가 많이 필요합니다. 따라서 각 곱셈 후에 키 전환을 구현하면 암호문이 압축될 수 있지만 약간의 소음이 발생합니다. .
모듈러스 전환: 곱셈이든 키 전환이든 노이즈는 기하급수적으로 증가합니다. 모듈러스 q는 앞서 언급한 Mod 10000입니다. 매개변수는 q가 클수록 더 많은 노이즈를 갖습니다. 여러 번 계산한 후에도 최종 노이즈는 여전히 q 내에 있으며 해독될 수 있습니다. 따라서 여러 작업 후에 노이즈 지수가 임계값을 초과하여 증가하는 것을 방지하기 위해 Modulus Switching을 사용하여 노이즈 예산을 줄여 노이즈를 억제할 수 있어야 합니다. 여기에서 기본 원리를 얻을 수 있습니다. 계산이 복잡하고 회로 깊이가 크다면 여러 기하급수적으로 증가한 후 가용성을 수용하기 위해 더 큰 모듈러스 q 잡음 예산이 필요합니다.
부트스트랩: 그러나 무한 깊이 계산을 수행하려는 경우 Modulus는 노이즈 증가만 제한할 수 있지만 각 스위치는 q 범위를 줄이면 계산의 복잡성이 더 작아져야 함을 의미합니다. 줄인. 부트스트랩은 노이즈를 줄이는 것이 아니라 노이즈를 원래 수준으로 재설정하는 참신한 기술입니다. 부트스트랩은 모듈러스를 줄일 필요가 없으므로 시스템의 컴퓨팅 성능을 유지할 수 있습니다. 그러나 단점은 많은 컴퓨팅 리소스가 필요하다는 것입니다.
일반적으로 제한된 단계의 계산의 경우 Modulus Switching을 사용하면 노이즈를 줄일 수 있지만 모듈러스, 즉 노이즈 예산도 감소하여 컴퓨팅 기능이 압축됩니다. 따라서 이는 제한된 단계의 계산에만 해당됩니다. Bootstrap은 노이즈 재설정을 구현할 수 있으므로 LHE 알고리즘을 기반으로 진정한 FHE, 즉 모든 기능의 무한 계산을 달성할 수 있으며 이것이 Fully of FHE의 의미이기도 합니다.
그러나 많은 양의 컴퓨팅 리소스가 필요하다는 단점도 분명합니다. 따라서 일반적인 상황에서는 이 두 가지 노이즈 감소 기술을 조합하여 사용합니다. 모듈러스 스위칭은 일상적인 노이즈 관리에 사용되며 지연에는 부트스트랩 시간이 필요합니다. 계산 비용이 더 많이 드는 부트스트랩은 모듈러스 전환이 노이즈를 더 효과적으로 제어할 수 없을 때 사용됩니다.
현재 FHE 솔루션에는 다음과 같은 특정 구현이 있으며, 모두 Bootstrap 핵심 기술을 사용합니다.
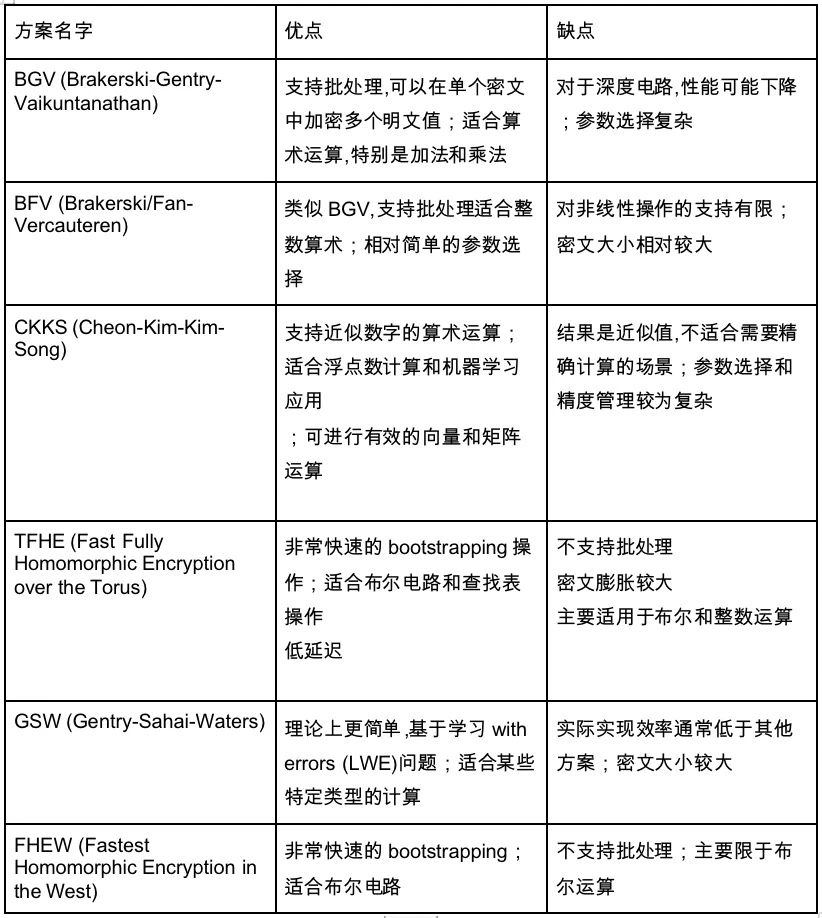
이것은 또한 우리가 언급하지 않은 회로 유형으로 이어집니다. 위에서 소개한 주요 회로는 산술 회로입니다. 그러나 또 다른 유형의 회로, 즉 부울 회로가 있습니다. 산술 회로는 1+1과 같이 상대적으로 추상적입니다. 노드도 덧셈 또는 나눗셈인 반면 부울 회로의 모든 숫자는 01진수로 변환되며 모든 노드는 NOT, OR 및 AND 연산을 포함한 부울 연산입니다. 우리의 컴퓨터 회로 구현과 유사합니다. 산술회로는 추상회로이다.
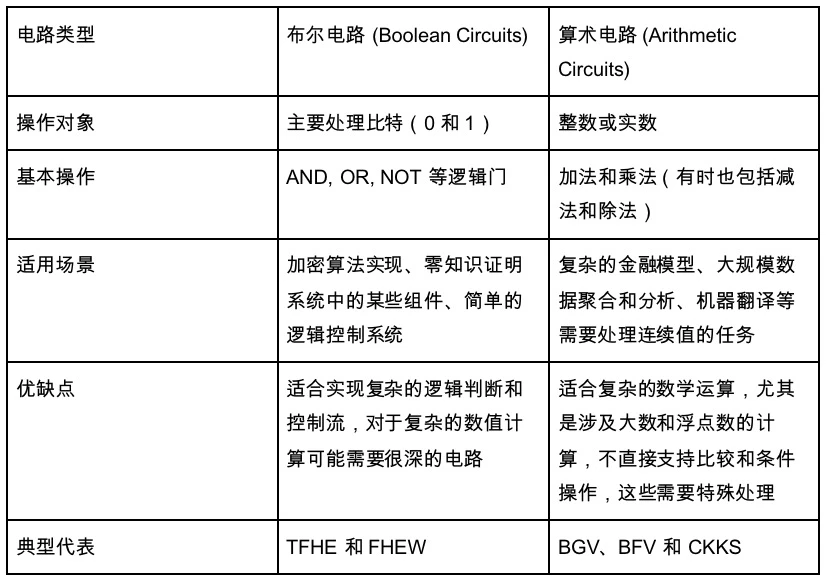
따라서 부울 연산은 덜 데이터 집약적인 유연한 처리로 대략적으로 생각할 수 있는 반면, 산술 연산은 데이터 집약적인 애플리케이션을 위한 솔루션입니다.
FHE가 직면한 문제
우리의 계산은 암호화된 후 회로로 변환되어야 하고, 단순 계산은 2+4만 계산하기 때문에 암호화 후에는 수많은 암호화 간접 계산 프로세스가 도입되고 다음과 같은 일부 최첨단 기술이 도입됩니다. 노이즈 문제를 해결하기 위한 부트스트랩으로, 결과적으로 계산 비용이 일반 계산보다 N배 더 높습니다.
우리는 독자들이 컴퓨팅 리소스에 대한 이러한 추가 암호화 프로세스의 오버헤드를 느낄 수 있도록 실제 사례를 사용합니다. 3GHz 프로세서에서 일반 계산에 200클럭 사이클이 걸린다고 가정하면 일반 AES-128 암호 해독에는 약 67나노초(200/3GHz)가 걸립니다. FHE 버전은 35초가 소요되는데, 이는 일반 버전(35/67 e-9)보다 약 522,388,060배 더 길다. 즉, 동일한 컴퓨팅 리소스, 동일한 일반 알고리즘 및 FHE 계산 알고리즘을 사용하면 컴퓨팅 리소스 요구 사항이 약 5억 배입니다.

DARPA dprive 프로그램, 출처: DARPA
데이터 보안을 위해 미국 DARPA는 2021년에 특별히 Dprive 프로그램을 구축하여 Microsoft, Intel 등 여러 연구팀을 초청했습니다. 그들의 목표는 FHE 가속기 및 지원 소프트웨어 스택을 만들어 FHE 컴퓨팅 속도를 높이는 것입니다. 암호화되지 않은 데이터에 대한 유사한 작업을 통해 FHE 계산 속도가 일반 계산의 약 1/10이 되는 목표를 달성합니다. DARPA 프로그램 관리자인 Tom Rondeau는 FHE 세계에서 우리의 계산은 일반 텍스트 세계보다 약 백만 배 느린 것으로 추정됩니다.
Dprive는 주로 다음 측면에 중점을 둡니다.
프로세서 단어 길이 늘리기: 최신 컴퓨터 시스템은 64비트 단어 길이를 사용합니다. 즉, 숫자는 최대 64비트일 수 있지만 실제로 q는 종종 1024비트입니다. 이를 달성하려면 q를 분할해야 합니다. , 이는 메모리 리소스에 영향을 미칩니다. 따라서 더 큰 q를 달성하려면 워드 크기가 1024비트 이상인 프로세서를 구축해야 합니다. 유한 필드 q는 매우 중요하며 앞서 언급했듯이 크기가 클수록 더 많은 단계를 계산할 수 있으므로 부트스트랩 작업을 최대한 연기할 수 있으므로 전체 컴퓨팅 리소스 소비가 줄어듭니다. q는 보안, 성능, 수행할 수 있는 계산량, 필요한 메모리 리소스를 포함하여 체계의 거의 모든 측면에 영향을 미치는 FHE에서 중심적인 역할을 합니다.
ASIC 프로세서 구축: 앞서 언급했듯이 병렬화의 용이성 및 기타 이유로 다항식을 구성하고 다항식을 통해 회로를 구축했습니다. 이는 ZK와 유사합니다. 현재 CPU와 GPU에는 회로를 실행할 수 있는 이러한 기능(컴퓨팅 리소스 및 메모리 리소스)이 없으며 FHE 알고리즘을 허용하려면 특수 ASIC 프로세서를 구축해야 합니다.
병렬 아키텍처 MIMD 구축 SIMD 병렬 아키텍처와 달리 SIMD는 여러 데이터에 대해 단일 명령, 즉 데이터 분할 및 병렬 처리만 실행할 수 있지만 MIMD는 데이터를 분할하고 계산을 위해 다른 명령을 사용할 수 있습니다. SIMD는 주로 데이터 병렬 처리에 사용되며, 이는 대부분의 블록체인 프로젝트에서 트랜잭션 병렬 처리를 위한 주요 아키텍처이기도 합니다. MIMD는 다양한 유형의 병렬 작업을 처리할 수 있습니다. MIMD는 기술적으로 더 복잡하며 동기화 및 통신 문제에 중점을 두어야 합니다.
DARPA의 DEPRIVE 프로그램 종료까지 한 달밖에 남지 않았다. Dprvie의 원래 계획은 2021년에 시작하여 2024년 9월에 3단계 계획을 종료하는 것이었습니다. 그러나 진행 속도가 느리고 여전히 예상에 미치지 못하는 것 같습니다. 목표는 일반 계산에 비해 1/10 효율성입니다.
FHE 기술 파괴의 진행 속도는 ZK 기술과 마찬가지로 느리지만, 기술 구현을 위해서는 하드웨어 구현이 필수라는 심각한 문제에 직면해 있습니다. 그러나 우리는 장기적으로 FHE 기술이 특히 첫 번째 부분에 나열된 일부 보안 데이터의 개인 정보를 보호하는 데 여전히 고유한 중요성을 갖고 있다고 믿습니다. DARPA의 경우 국방부는 대량의 민감한 데이터를 보유하고 있습니다. AI 일반 기능을 군대에 공개하려면 데이터 보안의 형태로 AI를 훈련해야 합니다. 뿐만 아니라 의료 및 금융과 같은 주요 민감한 데이터에도 적용 가능합니다. 실제로 FHE는 모든 일반 계산에 적합하지 않지만 민감한 데이터의 컴퓨팅 요구에 더 중점을 둡니다. 포스트퀀텀 시대.
이러한 첨단 기술의 경우 투자 주기와 상용화 사이의 시차를 고려해야 합니다. 그러므로 FHE의 시행 시기에 대해서는 매우 신중할 필요가 있다.
블록체인의 결합
블록체인에서 FHE는 주로 데이터의 개인정보 보호를 위해 사용됩니다. 적용 분야에는 온체인 개인정보 보호, AI 훈련 데이터 개인정보 보호, 온체인 투표 개인정보 보호, 온체인 개인정보 거래 검토 등이 포함됩니다. 그 중 FHE는 온체인 MEV 솔루션의 잠재적인 솔루션 중 하나로도 알려져 있습니다. MEV 기사 Illuminating the Dark Forest - Uncovering the Mystery of MEV 에 따르면 현재의 많은 MEV 솔루션은 MEV 아키텍처를 재구축하는 방법일 뿐이며 실제로 샌드위치 공격은 UX 문제를 야기합니다. 아직 해결되지 않았습니다. 처음에 우리가 생각한 해결책은 상태를 공개하면서 거래를 직접 암호화하는 것이었습니다.
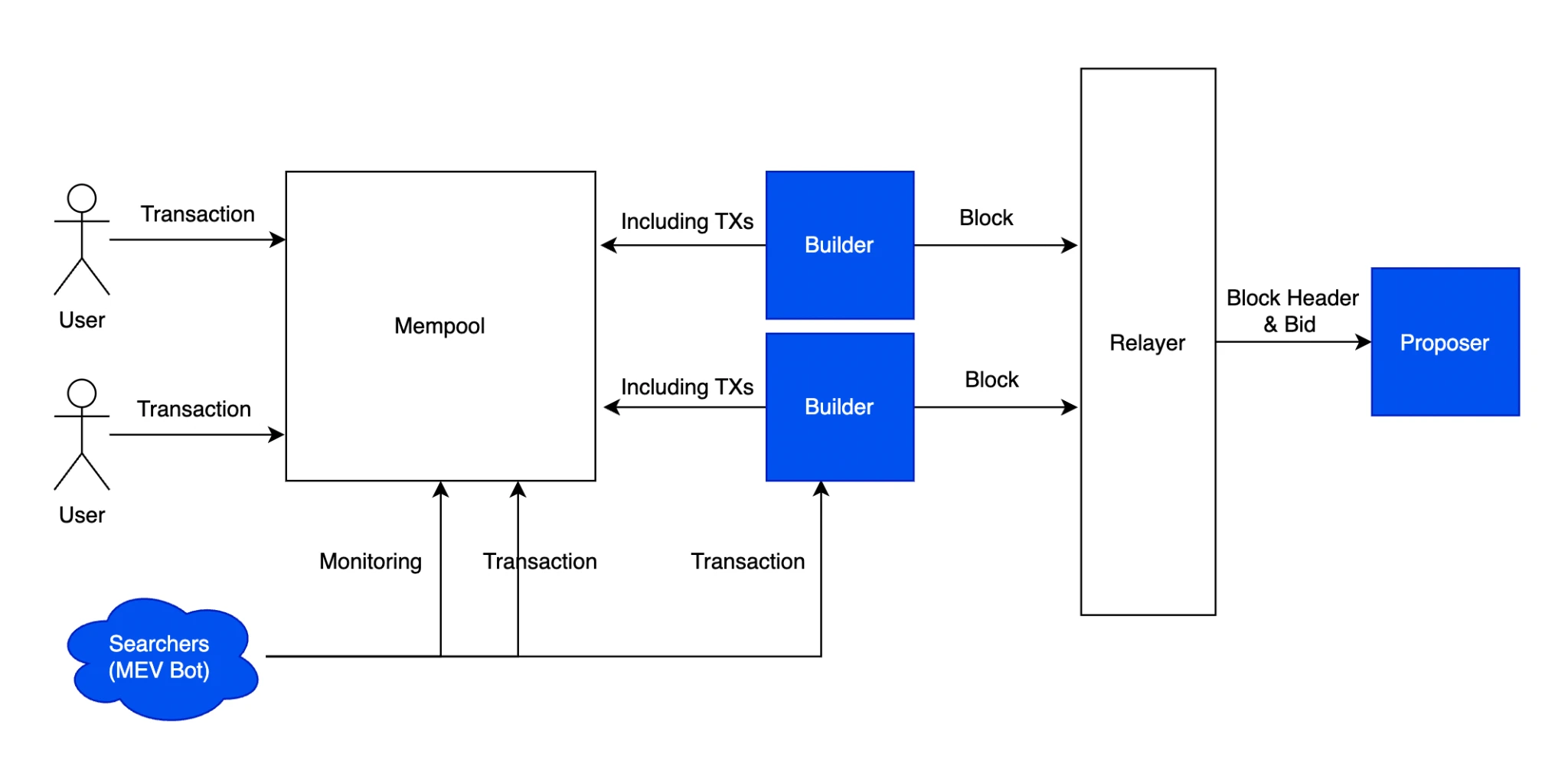
MEV PBS 공정
하지만 트랜잭션을 완전히 암호화하면 MEV 봇이 가져오는 긍정적인 외부효과가 동시에 사라지는 문제도 있습니다. FHE를 수행하려면 검증자 Builder가 가상 머신을 기반으로 실행되어야 하며 검증자도 필요합니다. 최종 상태의 정확성을 확인하면 노드 실행에 대한 요구 사항이 크게 증가하여 전체 네트워크의 처리량이 100만 배 느려집니다.
주요 프로젝트
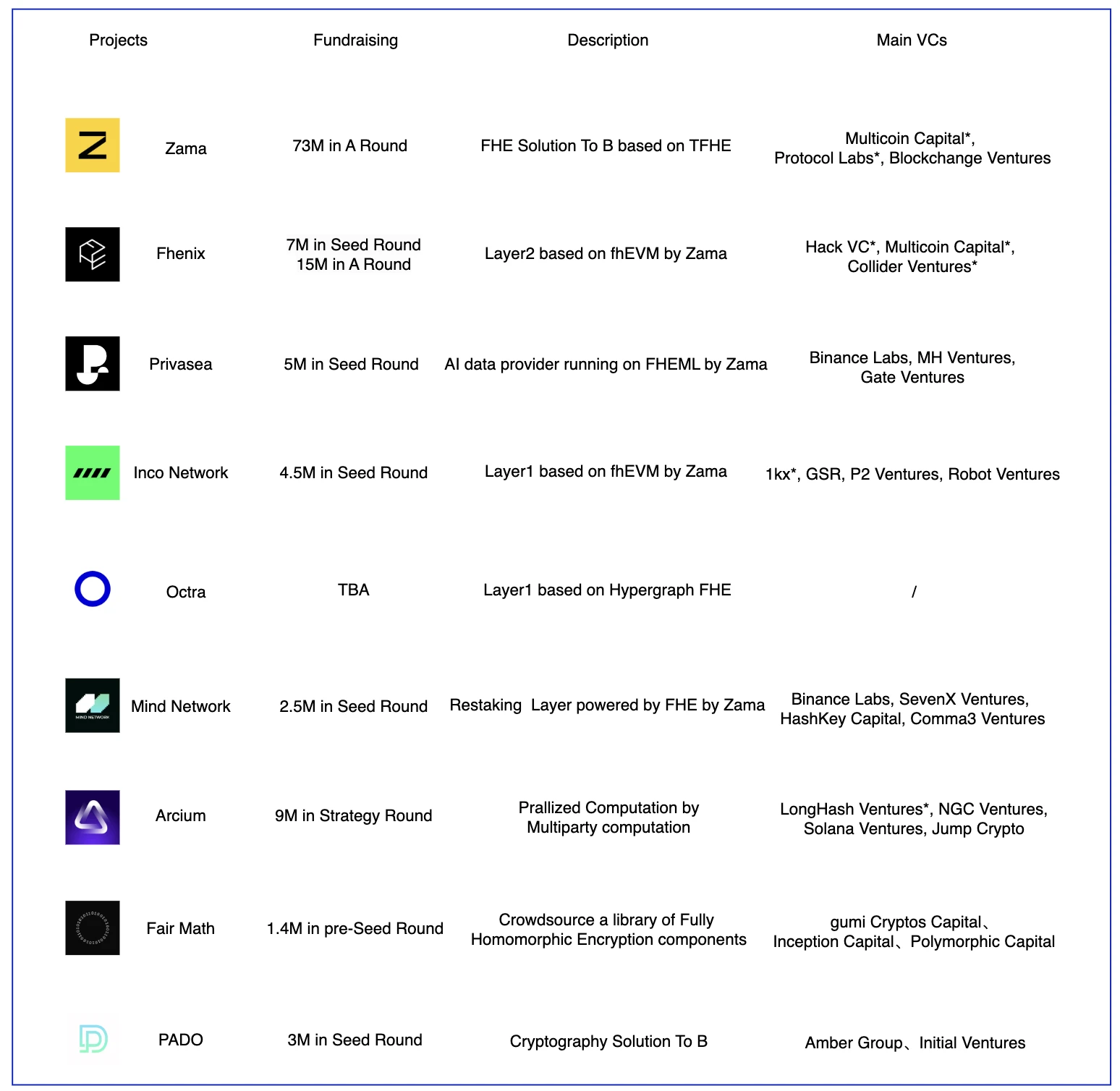
FHE 풍경
FHE는 비교적 새로운 기술입니다. 현재 프로젝트에서 사용되는 FHE 기술의 대부분은 Fhenix, Privasea, Inco Network 및 Mind Network와 같이 Zama에서 구축한 것입니다. Zama의 FHE 엔지니어링 구현 능력은 이러한 프로젝트에서 인정받았습니다. 위 프로젝트의 대부분은 Zama가 제공하는 라이브러리를 기반으로 구축되었습니다. 주요 차이점은 비즈니스 모델에 있습니다. Fhenix는 개인 정보 보호 우선 Optimism Layer 2를 구축하기를 희망하고 Privasea는 FHE의 기능을 사용하여 LLM 데이터 작업을 수행하기를 희망합니다. 그러나 이는 FHE에 대해 매우 높은 기술 및 하드웨어 요구 사항이 필요한 매우 데이터 집약적인 작업입니다. TFHE 기반은 최적의 선택이 아닐 수도 있습니다. Inco Network와 Fhenix는 모두 fhEVM을 사용하지만 하나는 Layer 1에, 다른 하나는 Layer 2에 구축되었습니다. Arcium은 FHE, MPC 및 ZK를 포함한 여러 암호화 기술의 융합을 기반으로 구축되었습니다. Mind Network의 비즈니스 모델은 상당히 다릅니다. 경제적 보안 문제를 해결하기 위해 Restake 트랙을 선택하고 FHE 기반의 서브넷 아키텍처와 유동성 보안을 제공하여 합의 계층에서 신뢰를 투표합니다.
자마
Zama는 TFHE 기반 솔루션으로, 부울 연산 및 낮은 단어 길이의 정수 연산 처리에 중점을 둔 Bootstrap 기술을 사용하는 것이 특징입니다. FHE 솔루션에서 더 빠른 기술 구현이지만 여전히 비교 대상이 있습니다. 둘째, 임의의 계산을 구현하는 것이 불가능합니다. 데이터 집약적인 작업에 직면하면 이러한 작업으로 인해 회로 깊이가 너무 커져 처리할 수 없게 됩니다. 이는 데이터 집약적인 솔루션이 아니며 암호화 프로세스의 특정 중요한 단계에만 적용됩니다.
TFHE는 현재 기성 구현 코드를 가지고 있습니다. Zama의 주요 작업은 rs-TFHE 크레이트인 Rust 언어를 사용하여 TFHE를 다시 작성하는 것입니다. 동시에 사용자가 Rust를 사용하는 임계값을 낮추기 위해 Python을 동등한 rs-TFHE로 변환할 수 있는 트랜스컴파일 도구 Concrate도 구축했습니다. 이 도구를 사용하면 Python 기반의 대규모 모델 언어를 TFHE-rs 기반의 Rust 언어로 번역할 수 있습니다. 이런 방식으로 동형암호 기반의 대규모 모델을 실행할 수 있지만, 현재로서는 데이터 집약적인 작업은 실제로 TFHE 시나리오에 적합하지 않습니다. Zama의 제품인 fhEVM은 FHE(완전동형암호)를 사용하여 EVM에서 기밀 스마트 계약을 구현하는 기술이며, Solidity 언어를 기반으로 컴파일된 엔드투엔드 암호화 스마트 계약을 지원할 수 있습니다.
일반적으로 To B 제품으로서 Zama는 TFHE를 기반으로 비교적 완전한 블록체인 + AI 개발 스택을 구축했습니다. 이는 web3 프로젝트가 FHE 인프라 및 애플리케이션을 쉽게 구축하는 데 도움이 될 수 있습니다.
옥트라
Octra의 특별한 점은 FHE를 구현하기 위해 다른 기술을 사용한다는 것입니다. 부트스트랩을 구현하기 위해 하이퍼그래프라는 기술을 사용합니다. 또한 부울 회로를 기반으로 하지만 Octra는 하이퍼그래프 기반 기술이 보다 효율적인 FHE를 달성할 수 있다고 믿습니다. 이는 FHE를 구현하기 위한 Octra의 원천 기술이며, 팀은 매우 강력한 엔지니어링 및 암호화 역량을 보유하고 있습니다.
Octra는 OCaml, AST, ReasonML(Octra 블록체인 네트워크와 상호 작용하는 스마트 계약 및 애플리케이션을 위해 특별히 설계된 언어) 및 C++와 같은 코드 라이브러리를 사용하여 개발된 새로운 스마트 계약 언어를 구축했습니다. 그것이 구축하는 Hypergraph FHE 라이브러리는 모든 프로젝트와 호환됩니다.
아키텍처도 Mind Network, Bittensor, Allora와 같은 프로젝트와 유사합니다. 메인 네트워크를 구축한 후 다른 프로젝트가 서브넷이 되어 상호 격리된 운영 환경을 구축합니다. 동시에 이러한 프로젝트와 유사하게 그들은 아키텍처 자체에 더 적합한 새로운 합의 프로토콜을 구축했습니다. Octra는 본질적으로 DAG(Directed Acycling Graph)를 기반으로 하는 기계 학습을 기반으로 하는 합의 프로토콜 ML 합의를 구축했습니다. .
이번 합의의 기술적 원리는 아직 공개되지 않았지만 대략적으로 추측할 수는 있다. 아마도 트랜잭션이 네트워크에 제출된 다음 SVM(Support Vector Machine) 알고리즘을 사용하여 주로 각 노드의 현재 네트워크 부하를 기반으로 최상의 처리 노드를 결정합니다. 시스템은 과거 데이터(ML 알고리즘 학습)를 기반으로 최상의 상위 노드 합의 경로를 결정합니다. 노드의 1/2만 만족하면 데이터베이스 증가에 대한 합의에 도달할 수 있습니다.
예상하다
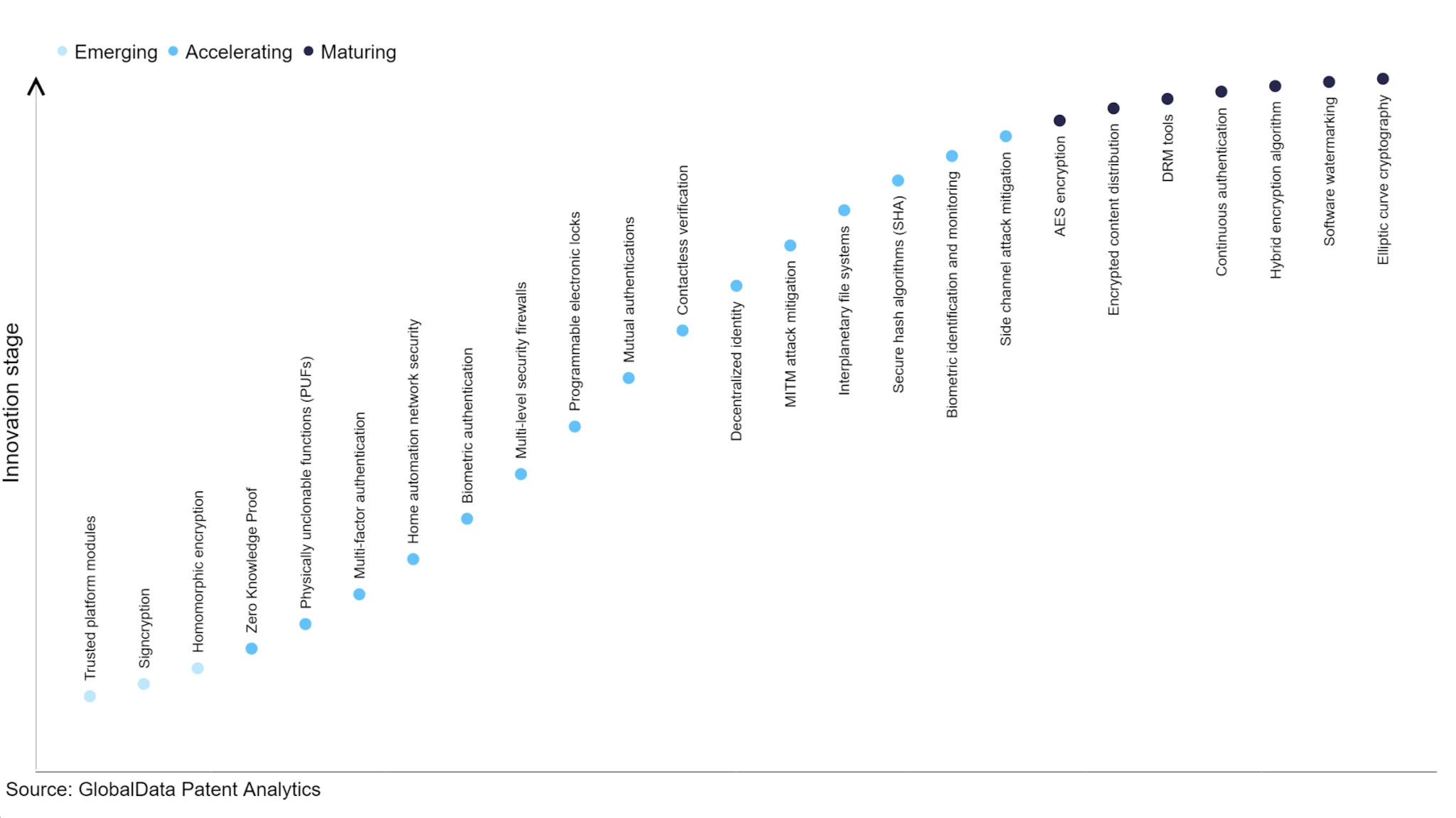
최첨단 암호기술 개발현황, 출처 : 평결
FHE 기술은 미래지향적 기술로, 아직 ZK 기술에 비해 개발 상태가 열악하고, 개인 정보 보호로 인한 낮은 효율성과 높은 비용으로 인해 대부분의 상업 조직에서는 의욕이 부족합니다. Crypto VC의 투자로 인해 ZK 기술의 발전은 더욱 빨라졌습니다. FHE는 아직 초기 단계에 있으며, 지금도 높은 비용, 높은 엔지니어링 난이도, 불분명한 상용화 전망으로 인해 시장에 나와 있는 프로젝트가 거의 없습니다. 2021년 DAPRA는 Intel, Microsoft 등 여러 회사와 협력하여 42개월 FHE 공격 계획을 시작했습니다. 일부 진전이 있었지만 아직 달성한 성능 목표에는 미치지 못합니다. Crypto VC가 이러한 방향에 주목함에 따라 업계에 더 많은 자금이 쏟아질 것으로 예상되며, Zama 및 Octra A와 같은 강력한 엔지니어링 및 연구 역량을 갖춘 프로젝트도 더 많이 나타날 것으로 예상됩니다. FHE 기술과 블록체인의 상용화 및 개발 현황의 결합은 여전히 검토할 가치가 있지만 검증 노드 투표의 익명화는 여전히 적용 범위가 좁습니다.
ZK와 마찬가지로 FHE 칩의 구현은 FHE 상용화를 위한 전제 조건 중 하나입니다. 현재 Intel, Chain Reaction, Optalysys 등 많은 제조업체에서 이 측면을 검토하고 있습니다. FHE가 많은 기술적 저항에 직면하더라도 FHE 칩의 구현으로 완전 동형 암호화는 큰 가능성과 정확한 수요가 있는 기술로서 국방, 금융, 의료 등 산업에 엄청난 변화를 가져올 것이며, 이러한 개인 데이터를 미래의 양자 알고리즘과 같은 기술과 결합하는 것도 폭발적인 순간을 가져올 것입니다.
우리는 이 초기 최첨단 기술을 기꺼이 탐구할 의향이 있습니다. 상용화 가능한 FHE 제품을 구축하고 있거나 보다 최첨단 기술 혁신을 갖고 있다면 저희에게 연락을 환영합니다!










