當人工智慧越過圖靈門檻,區塊鏈重建信任結構,數據本身正悄悄取代能源,成為新一輪文明躍遷的核心資源。然而,在這場浩大的科技進程中,我們才剛意識到一個古老的問題正在捲土重來:人類是否還能擁有真正的隱私?
The greatest enemy of knowledge is not ignorance, it is the illusion of knowledge. ——Stephen Hawking
隱私計算(Privacy Computing)由此而生。它不是某項孤立技術的突變,而是密碼學、分散式系統、人工智慧與人類價值之間長期博弈的結果。自 20 世紀末多方安全計算、同態加密等理論架構提出以來,隱私計算逐漸演變為應對「資料失控」時代的關鍵護欄——它讓我們在不暴露原始資料的前提下,仍能合作計算、共享價值、重建信任。
這是一段仍在發生的技術史,更是一場關於「自由意志能否在演算法世界中存活」的哲學提問。而隱私計算,也許正是通往答案的第一扇門。
一、萌芽期(1949 年– 1982 年):現代密碼學的起點
1949 年:香農與資訊理論的開端
1949 年,克勞德·香農在論文《保密系統的通訊理論》中首次以嚴格的數學方法系統地分析了通訊系統的安全性。他利用資訊理論方法定義了“完善保密性”,指出只有一次性密碼本(one-time pad)能夠滿足這種嚴格意義上的安全需求。香農的研究方法極為嚴謹,從數學原理出發,運用機率論和統計學方法建立保密系統模型。他明確了熵和資訊量的概念,奠定了現代密碼學的理論基礎。
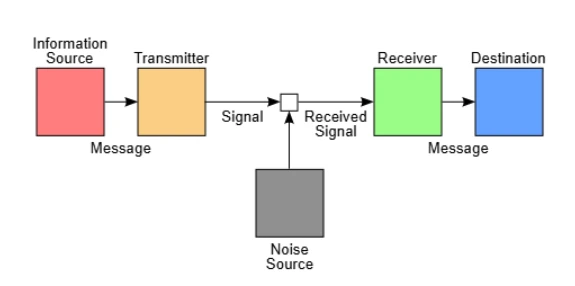
香農在 1948 年論文《通訊的數學理論》中提出的經典通訊模型,展示了資訊來源、編碼器、通道、解碼器和資訊接收者之間的關係
香農的研究過程富有創造性,他在貝爾實驗室工作期間,不僅致力於理論研究,也進行大量的實驗驗證。他習慣用直覺的類比來解釋複雜概念,例如將訊息傳輸類比成水流、熵類比成不確定性。據趣聞所載,他也曾在實驗室走廊騎獨輪車來放鬆和激發創造力。這篇論文的影響深遠,不僅奠定了現代密碼學的理論基礎,也影響了後續幾十年間整個資訊安全領域的研究路徑。
1976 年:Diffie-Hellman 的突破
1976 年,Whitfield Diffie 和 Martin Hellman 在《密碼學新方向》一文中提出了公鑰加密的概念,設計了 Diffie-Hellman 金鑰交換協定。這項協議的研究方法是基於離散對數問題的數學難題,兩人首次提出了無需預先共享秘密即可安全交換密鑰的方案。
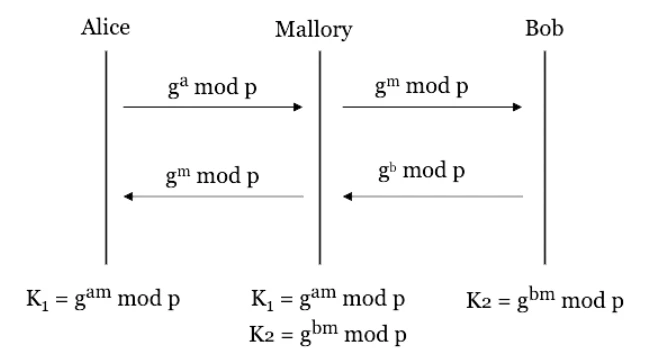
該圖展示了 Diffie-Hellman 金鑰交換的基本流程,Alice 和 Bob 透過公開的通道交換信息,最終生成共享的金鑰,而不被竊聽者得知
研究過程並非一帆風順,兩人花了多年時間不斷嘗試和失敗,在深入研究數學和數論基礎上,最終才找到適合的數學構造。 Diffie 因為與眾不同的外型和行事風格,在學術界也引起了不少趣聞軼事,例如會議組織者經常誤將他認作搖滾樂隊成員。這項工作從根本上改變了密碼學領域,為數位簽章和其他現代安全協議奠定了基礎。
1977 年: RSA 演算法誕生
1977 年,麻省理工學院的 Ron Rivest、Adi Shamir 和 Leonard Adleman 共同發明了著名的 RSA 演算法,這是第一個實用的非對稱加密演算法。他們的研究方法採用了大素數因子分解問題作為安全基礎,透過複雜的數學推導和電腦實驗成功建構出實用的非對稱加密機制。
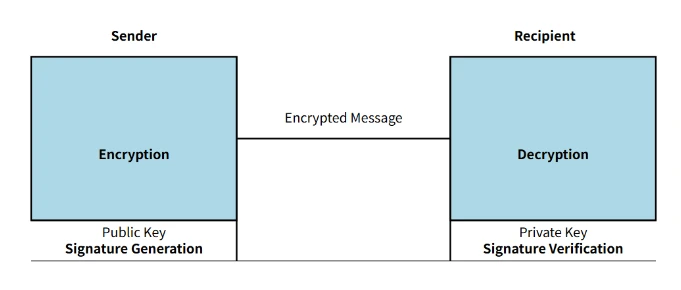
這張圖展示了 RSA 加密和解密的過程,包括公鑰和私鑰的生成,以及如何使用公鑰加密和私鑰解密訊息
研究過程中,Rivest 最初在經歷了一整夜的嘗試後突發靈感,迅速完成演算法草稿;而 Adleman 則負責了演算法實作和驗證。他們用 RSA 演算法加密了一條著名的訊息,挑戰同事解密,以此紀念這個重要時刻。 RSA 演算法不僅具有理論意義,更重要的是為電子商務、數位簽章等應用場景提供了實際的安全方案。
1978 年:同態加密的雛形
1978 年,Rivest、Shamir 和 Adleman 在提出 RSA 演算法後,又在探討加密資料的計算可能性,也就是同態加密的概念。他們提出問題時,只簡單指出一個加密系統能否允許密文直接進行運算而無需解密。雖然當時未能解決這個難題,但他們提出的這個前瞻性問題,卻引發了未來三十多年密碼學界的持續探索。

此圖展示了同態加密的概念,即在密文上直接進行運算,解密後得到的結果與在明文上運算的結果一致
1979 年– 1982 年:密碼學百花齊放
在此期間,密碼學領域迎來了許多開創性的理論研究成果。 Adi Shamir 提出了秘密分享方法,透過精妙的代數結構設計,使秘密訊息被多方安全管理,並且只有在特定數量的人參與時才可以重構秘密。
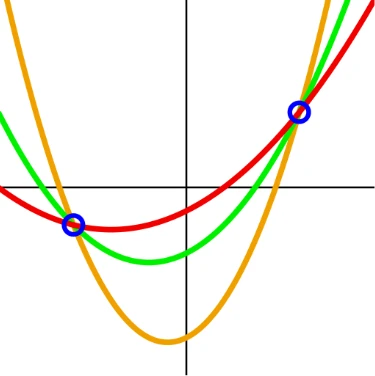
透過2 點可以繪製無數個2 次多項式。需要3 個點才能唯一確定一個2 次多項式。此圖僅供參考-Shamir 的方案使用有限域上的多項式,這在二維平面上不易表示
Michael Rabin 在研究中提出了不經意傳輸(Oblivious Transfer),這種協議巧妙解決了資訊交換中雙方的信任問題,使得一方能夠安全地獲取資訊而對方卻無法知曉具體內容。
姚期智在 1982 年提出了著名的“百萬富翁問題”,以詼諧而形象的方式,將複雜的密碼學思想直觀展示出來,描述如何在不暴露各自財富具體信息的情況下安全地確定誰更富有。姚期智的研究方法使用了抽象的邏輯推導和博弈論方法,這項研究直接啟發了後續安全多方計算(MPC)的研究熱潮,推動了密碼學在資訊共享、資料隱私保護等領域的廣泛應用。
這些豐富而深入的研究成果共同推動了現代密碼學領域的初步繁榮,為未來的技術演進奠定了堅實的基礎。
二、探索期(1983 年– 1999 年):理論爆發與隱私工具雛形
1985 年:零知識證明的誕生
1985 年,麻省理工學院的 Shafi Goldwasser、Silvio Micali 和 Charles Rackoff 提出了零知識證明(Zero-Knowledge Proof,ZKP)的概念。他們在研究互動式證明系統的基礎上,提出了一個問題:如何證明自己知道某個秘密而不洩露這個秘密本身。他們運用複雜的交互協議和機率論方法,設計出證明過程,讓驗證方能夠相信提供證明的人確實掌握某個信息,但同時又無法推斷出具體的信息細節。
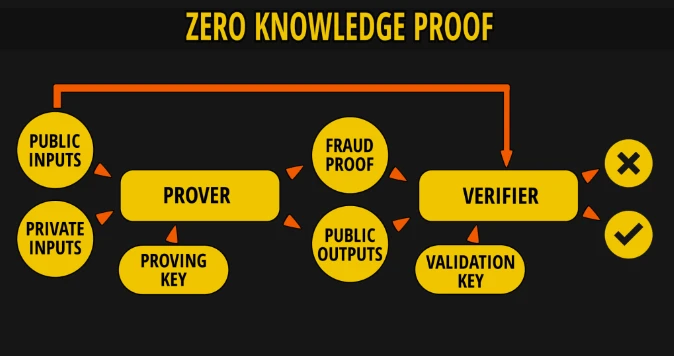
該圖展示了零知識證明的基本流程,證明者(Prover)向驗證者(Verifier)證明其擁有某個秘密訊息,但在此過程中不洩露該資訊本身
趣聞軼事是,這項研究的靈感最初來自一種簡單的紙牌遊戲,他們在一次學術會議上以互動遊戲的方式演示了零知識證明,讓現場觀眾既感到驚奇又頗為困惑。 ZKP 的提出,不僅為現代密碼學領域提供了重要理論工具,更是奠定了隱私計算中的重要技術支撐,對後續諸如匿名驗證、隱私保護、區塊鏈等領域產生了深遠影響。
1986 – 1987 年:安全多方計算的突破
1986 年,姚期智教授提出了混淆電路(Garbled Circuit)技術,巧妙地實現了兩方安全計算的協議。他將函數計算轉換成複雜電路,再將電路混淆後交由另一方執行,確保對方能計算出結果但無法窺視具體輸入資料。姚期智的研究方法將密碼學與計算複雜性理論融合,被視為電腦科學的突破。
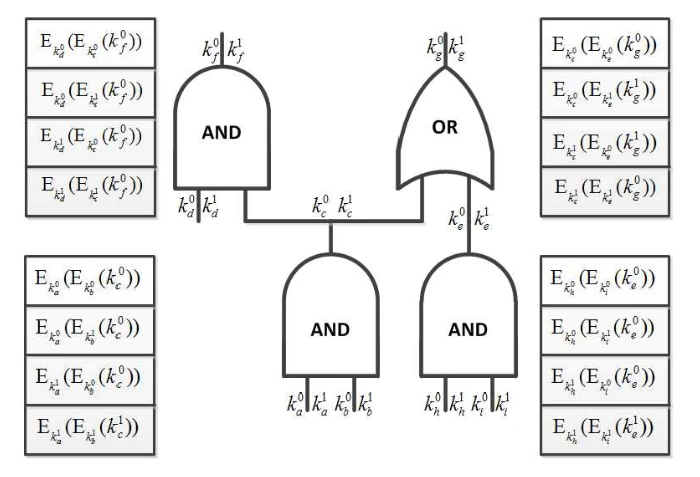
此圖展示了姚期智提出的混淆電路(Garbled Circuit)技術的基本結構,示範如何透過電路混淆實現兩方安全計算
趣聞是姚期智獨特的跨領域背景讓他常以意想不到的角度切入問題,被學界戲稱為密碼學界的「黑魔法」。緊隨其後, 1987 年,Oded Goldreich、Silvio Micali 和 Avi Wigderson 提出了著名的 GMW 協議,將安全多方計算(MPC)擴展到多方場景,實現多個參與者在不暴露各自輸入資料情況下安全執行計算。這些成果實質地推動了安全多方計算的理論和實際發展,使得隱私計算逐步從理論走向可能。
1996 年:聯邦學習的早期設想
1996 年,David W. Cheung 提出了用於分散式系統中的關聯規則挖掘演算法,雖然當時並未明確提出聯邦學習這個術語,但他研究的核心思想與後來流行的聯邦學習思想不謀而合。他提出的分散式資料探勘方法,不要求將所有資料集中在一起,而是讓多個獨立的資料擁有者各自處理資料並交換挖掘結果。
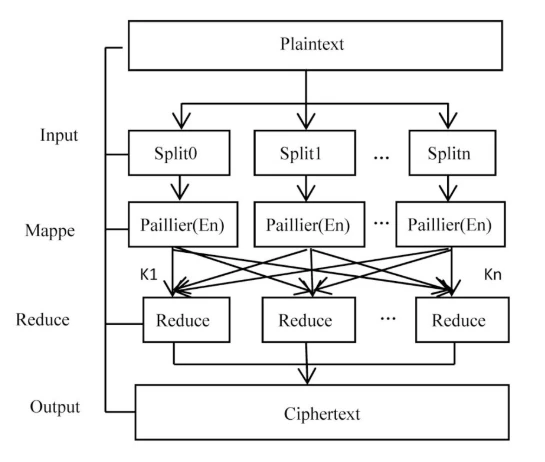
此圖展示了 Paillier 加密方案的平行加密過程,說明如何在密文狀態下進行加法運算
Cheung 的研究過程也相當有趣,他最初是為了解決大型企業內部資料探勘的難題,卻無意中為未來的聯邦學習提供了理論原型。當時他的研究並未引起廣泛關注,直到 20 多年後,隨著隱私問題日益凸顯,Google 等公司開始大規模採用聯邦學習,這項成果才真正展現出其前瞻性。
1999 年:加法同態加密的實用化
1999 年,Pascal Paillier 提出了一種新的加法同態公鑰加密方案,允許密文直接進行加法運算而無需解密。這項研究解決了長期以來同態加密領域的實際應用瓶頸。他採用基於群論的數學構造,實現了安全的加法同態屬性,使得資料在密文狀態下仍能有效處理,顯著推動了加密資料應用場景的實際落地。
Paillier 方案廣泛應用於電子投票、隱私保護資料分析等實際情境。據悉,Paillier 在設計方案時最初的靈感來自於解決匿名電子投票中的隱私問題,這種需求驅動的研究方法,不僅具有理論意義,也極大促進了同態加密技術的產業化發展。
這一階段,密碼學理論大放異彩,各種新穎的技術與方法不斷湧現,為隱私計算的蓬勃發展奠定了堅實基礎,也為日後的技術應用提供了豐富的工具與方法。
三、成長期(2000 年– 2018 年):隱私計算框架成型
2006 年:差分隱私的開創
2006 年,微軟研究院的 Cynthia Dwork 提出了差分隱私(Differential Privacy)理論,這個創新理論為大數據時代的資料隱私保護提供了嚴格的數學保障。 Dwork 的研究方法巧妙地利用隨機雜訊加入資料查詢結果,使得單一資料記錄的加入或刪除對整體查詢結果的影響降到極低,從而有效保護了個別資料的隱私。
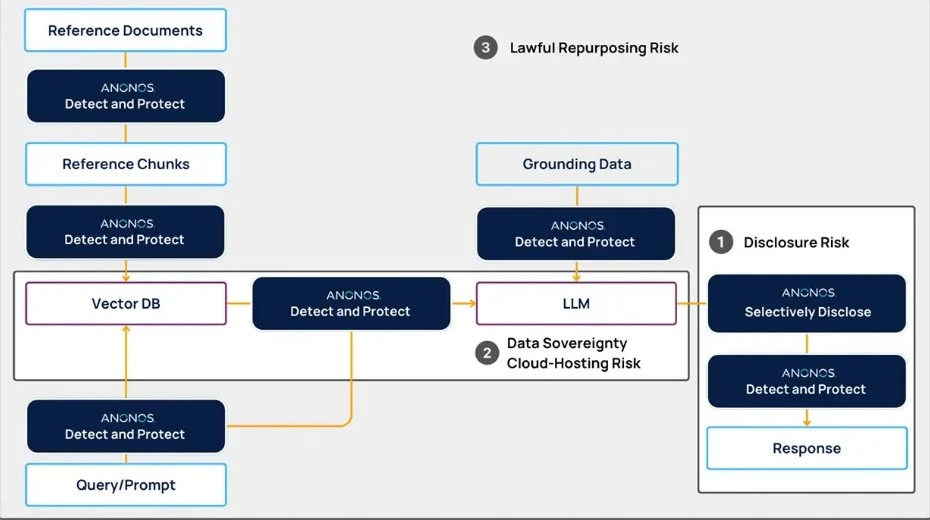
此圖展示了差分隱私的基本機制,透過在查詢結果中加入隨機噪聲,保護個別資料的隱私
有趣的是,Dwork 在早期推廣差分隱私時,曾用一本電話簿作為例子來生動地說明隱私洩露的現實風險。她指出,儘管匿名化處理後的資料看似安全,但結合外部資訊仍可能恢復敏感隱私。她的研究開創了資料隱私保護的新標準,被廣泛用於醫療資料、人口統計、社會科學研究等領域,深刻地影響了後續隱私計算技術的發展路徑。
2009 年:全同態加密與可信任執行環境(TEE)的突破
2009 年是密碼學技術發展的關鍵一年。首先,開放行動終端平台(OMTP)首次提出了可信任執行環境(TEE)的前身方案,試圖在硬體層面建置隔離安全環境,保護行動裝置敏感資料的安全性。
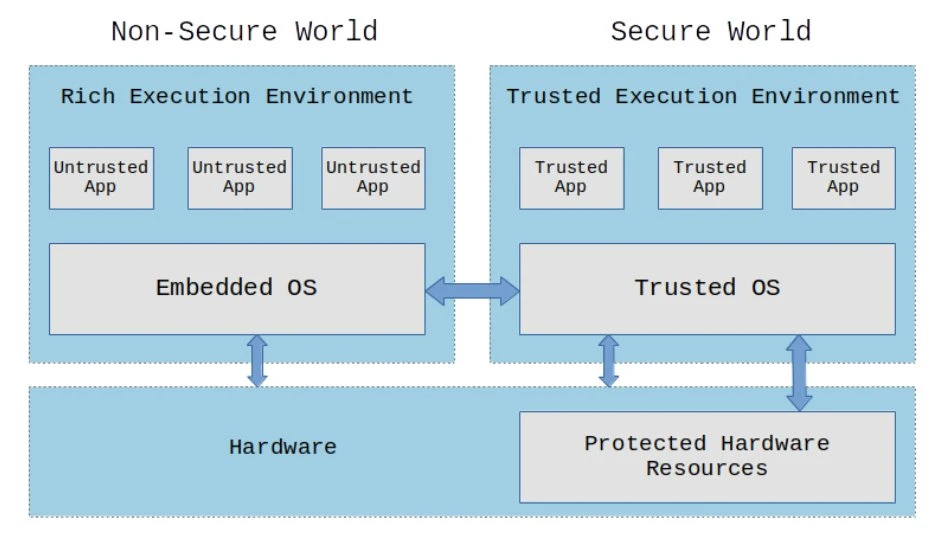
此圖展示了 TEE 的基本架構,說明如何在硬體層面上創建隔離的執行環境,保護敏感資料的安全
同年,IBM 的 Craig Gentry 提出了首個全同態加密(Fully Homomorphic Encryption, FHE)方案。這個理論允許資料在加密狀態下進行任意計算,無需解密即可獲得處理結果。 Gentry 的研究極富傳奇色彩,據傳他在多年研究陷入瓶頸後,某次偶然的散步中靈光乍現,最終攻克了困擾學界數十年的難題。他的突破開啟了密文運算的新篇章,讓加密資料在雲端運算、金融資料分析等場景中得到了安全且有效率的應用。
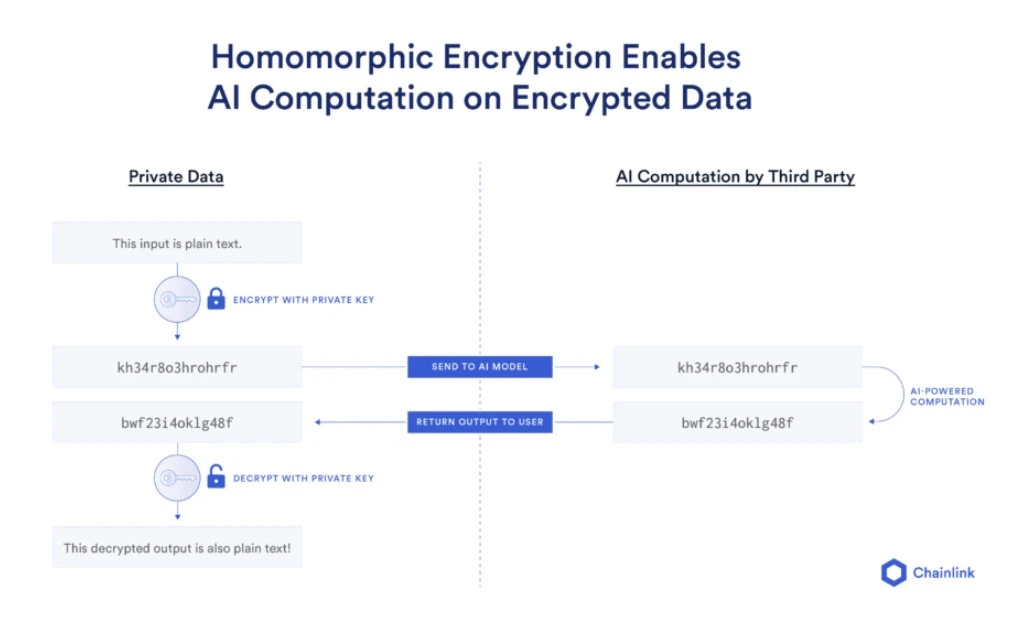
此圖展示了全同態加密的工作流程,說明如何在密文狀態下進行任意計算,並在解密後獲得正確結果
2013 年:醫療聯邦學習的先驅
2013 年,王爽教授團隊在隱私運算領域率先提出醫療聯邦學習系統 EXPLORER,這是首次在分散式醫療資料上實現安全模型訓練的實踐。團隊採用分散式機器學習與隱私保護技術結合的方式,設計出能跨機構合作而無需共享原始資料的模型訓練方法。
據報道,這項研究最初動機源於實際醫療研究中的資料共享困難問題,團隊在研究過程中經歷了多次技術迭代和跨學科合作,最終成功構建了能夠安全共享醫療數據而不洩露患者隱私的技術框架。 EXPLORER 系統迅速成為國際醫療資料安全保護的標桿,推動了全球醫療資料協作的新實踐。
2015 年– 2016 年:隱私運算產業化的標誌
2015 年至 2016 年,隱私運算迎來了產業化的里程碑。 Intel 公司發布了首個商業化的可信任執行環境技術 SGX(Software Guard Extensions),該技術允許應用程式在硬體層面進行隔離執行,確保敏感資料和程式的安全性。這項突破使隱私保護真正走入實際應用場景,例如安全雲端運算、金融交易等領域。
同時,Google AI 團隊在 2016 年提出了聯邦學習(Federated Learning)框架,將隱私運算概念直接融入手機終端應用中。聯邦學習允許資料在設備本地進行訓練,再將模型參數集中整合,無需直接上傳敏感資料。這項方法不僅提高了資料安全性,還顯著增強了使用者隱私保護能力。
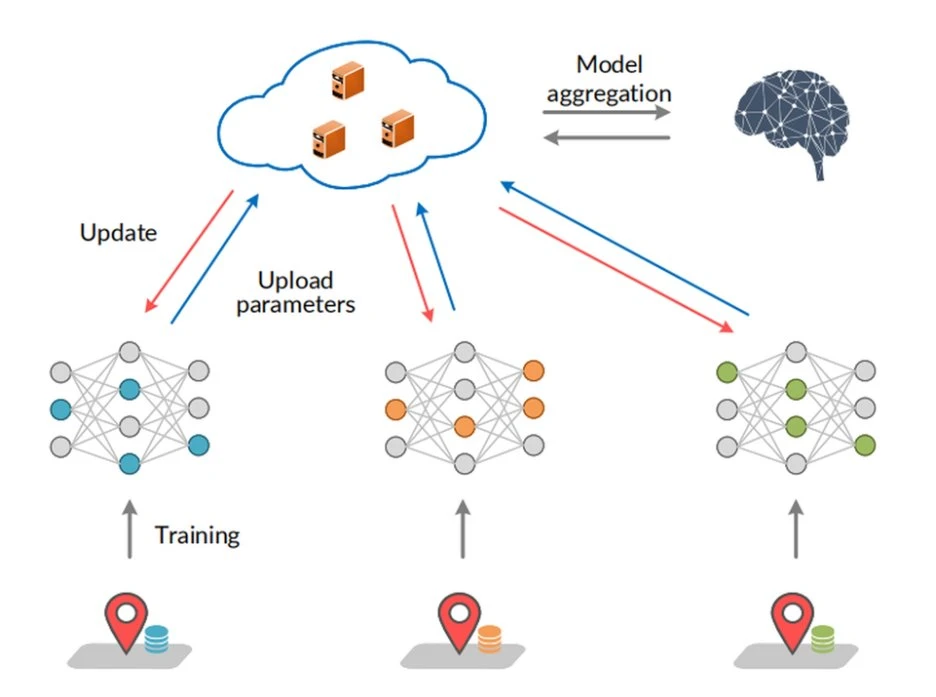
該圖展示了聯邦學習的基本流程,說明如何在不共享原始資料的情況下,透過本地模型訓練和參數聚合,實現分散式機器學習
有趣的是,Google 聯邦學習計畫最初的內部代號為“蜜蜂計畫”,寓意多個終端像蜜蜂一樣分別貢獻並彙聚成整體的智慧模型。這個生動的比喻也展示了隱私計算技術如何從抽象理論走向實際生活中的廣泛應用。
四、應用期間(2019 年– 2024 年):隱私計算走向實用
2019 年:聯邦遷移學習與 FATE 系統的誕生
2019 年,香港科技大學的楊強教授及其團隊正式推出聯邦遷移學習(Federated Transfer Learning)理論與開源系統 FATE(Federated AI Technology Enabler),極大地推動了聯邦學習技術的產業化與工程化進展。楊強團隊的研究創新地將聯邦學習與遷移學習結合,使不同領域、不同場景的資料在不共享原始資料的情況下實現模型遷移和知識共享,從而解決了資料孤島問題。
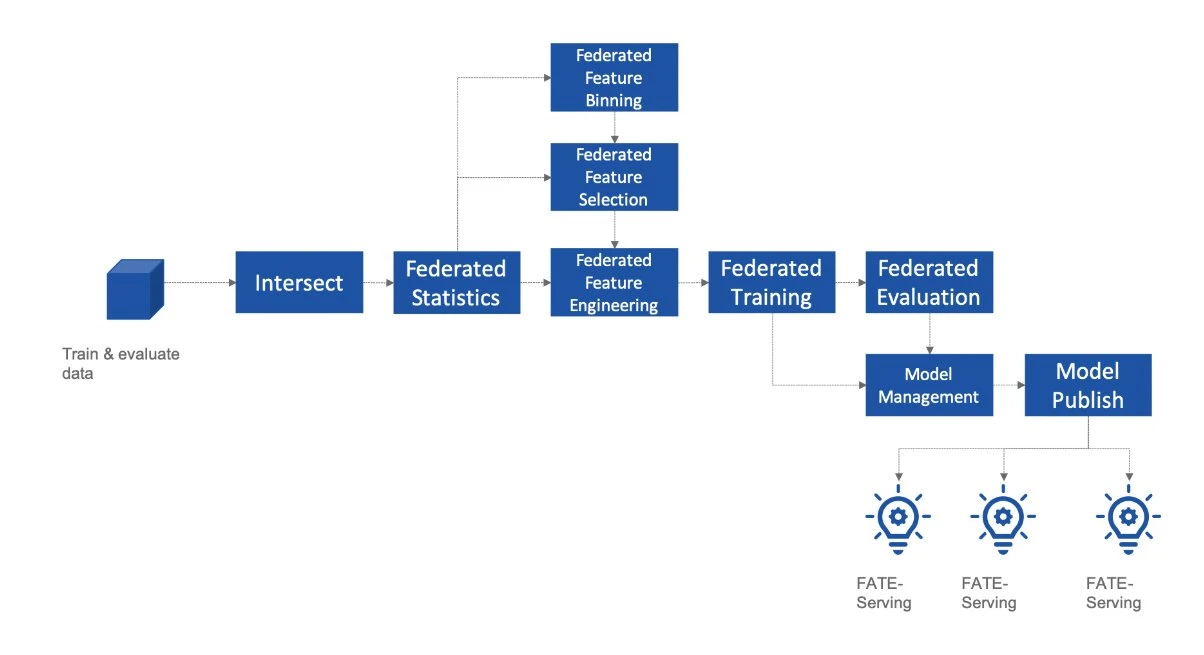
該圖展示了 FATE 系統的架構,說明如何透過聯邦學習實現跨機構的資料協作與模型訓練
趣聞軼事是,在 FATE 系統正式開源發布大會上,由於業界對這項技術的高度關注,參與人數遠超預期,以致於主辦單位不得不臨時更換更大的場地。這一軼事也反映出業界對聯邦學習落地應用的極大興趣與熱情。
FATE 系統的問世不僅推動了聯邦學習技術快速落地,更為後續的數據合作提供了技術框架,被迅速應用到金融風控、醫療診斷、智能政務等實際場景中,為數據共享與隱私保護提供了實質性解決方案。
隱私運算成為資料基礎設施
隨著資料時代的到來,資料要素市場快速發展,資料安全與隱私保護逐漸成為各產業關注的核心議題。同時,各國資料合規性要求持續提升,促使隱私運算技術迅速與金融、醫療、政務等重要產業深度整合。
在金融領域,隱私計算技術如同態加密(FHE)、安全多方計算(MPC)和零知識證明(ZKP)等技術被廣泛用於風險控制和反詐欺場景,確保資料使用安全合規。在醫療領域,差分隱私(DP)和聯邦學習(FL)技術有效地保護了病患隱私,促進了跨機構醫療研究和協作。
政務領域則積極採用可信賴執行環境(TEE)技術,建構安全高效的政務資料處理平台,保障敏感資訊安全及公共信任。這些技術的協同使用極大地提高了資料價值的釋放速度,提升了資料共享效率和安全性。
技術協同與產業融合
在當前階段,密碼學領域的多種核心技術,包括零知識證明(ZKP)、安全多方計算(MPC)、全同態加密(FHE)、可信任執行環境(TEE)、差分隱私(DP)和聯邦學習(FL)等逐步走向協同共生的發展路徑。這種技術融合不僅豐富了隱私保護的手段,更提升了隱私運算整體的實用性與可靠性。
隱私運算不再停留在理論研究階段,而是真正成為廣泛應用的基礎設施,支撐起資料要素的安全流通和價值共享,形成了以「隱私運算+產業」的新生態。未來,隱私運算技術將進一步融入各產業數位轉型過程中,成為推動產業創新、經濟發展和社會進步的重要引擎。
這些豐富的理論探索與技術落地案例,標誌著密碼學與隱私運算從理論研究真正走向實踐應用的新高度,也為高效能密碼應用的發展奠定了穩固的基礎。
五、密碼學走向千家萬戶(2025 年至今):ZEROBASE 階段
2025 年:ZEROBASE 的崛起與普惠隱私計算
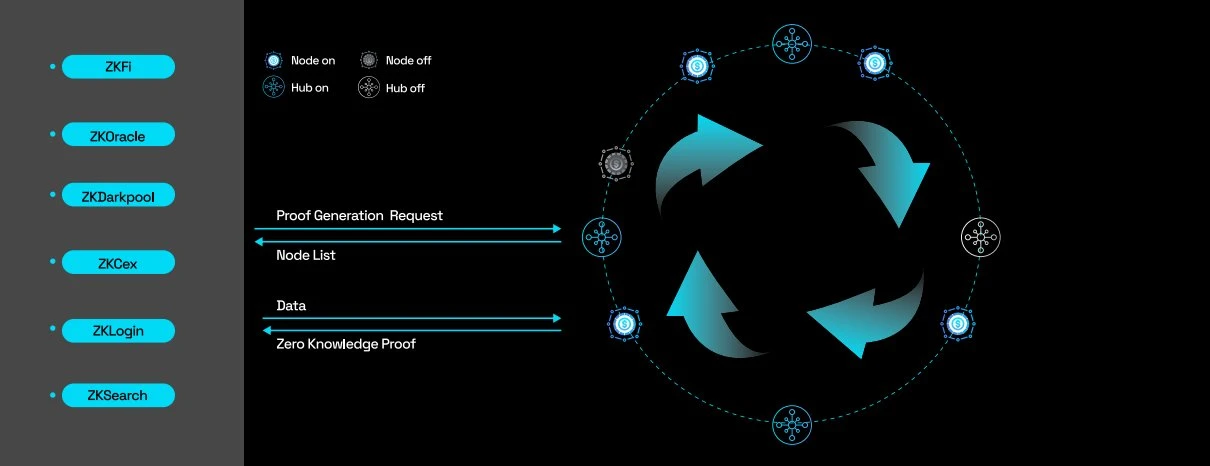
在 ZEROBASE 網路中,節點被劃分為不同的子集,每個子集由一個 HUB 管理。每個 HUB 只記錄其負責的 NODE 的狀態訊息,這意味著 NODE 只與其相應的 HUB 通訊。在這種架構中,即使 NODE 數量增加,透過添加更多 HUB,系統也可以繼續平穩運行
2025 年,隱私計算進入了一個全新階段-ZEROBASE 階段。 ZEROBASE 專案以其獨特的方式,將隱私運算帶入了一般使用者的日常生活中。 ZEROBASE 的願景是建立一個全球化的零知識(ZK)信任基礎設施,支援金融、政務、醫療等多個領域的隱私運算應用落地。
ZEROBASE 採用了一種去中心化、易用的架構,以降低使用者參與隱私運算的技術門檻。他重新設計了零知識證明(ZKP)系統的可信任設定流程,首次以瀏覽器結合影像熵來源的形式完成可信任設定(Trusted Setup)。

ZEROBASE 的吉尼斯世界記錄密碼學挑戰預熱活動頁面
2025 年初,ZEROBASE 發起了一項吉尼斯世界紀錄挑戰,在預熱階段成功吸引 564, 000 多名全球用戶在 OKX Wallet 參與預熱活動。
ZEROBASE:技術創新與社會共識
ZEROBASE 將複雜的技術透過使用者友善的互動方式呈現,僅需簡單的圖像上傳和瀏覽器操作,即可實現過去高度複雜的可信任設定。這種設計理念不僅降低了參與門檻,更將 ZK 技術變成了一項社會化活動,大大提升了大眾對隱私運算技術的認知與接受度。
在技術層面上,ZEROBASE 開發了高度優化的 ZKP 電路,實現了每秒超過 1000 次的證明產生速度,這使得 ZEROBASE 在 ZK 證明市場中迅速佔據領先地位。同時,ZEROBASE 也推出了多個創新應用,包括 zkLogin(無摩擦的Web3認證)、zkCEX(鏈上訂單匹配與鏈下結算的混合交易所模式)和 zkStaking(驗證套利風險、優化收益產生的抵押系統)。
ZEROBASE 金氏世界紀錄挑戰的重要意義
ZEROBASE 發起的金氏世界紀錄挑戰不僅是一場科技突破,更是一種社會敘事的轉變。與傳統的可信任設定儀式不同,ZEROBASE 這項挑戰將隱私計算從神秘的「黑盒子」變成了開放、透明、可參與的社會事件。透過大眾化的參與方式與公開透明的驗證流程,ZEROBASE 有效解決了 ZK 技術長期以來的信任與共識難題。

我真的很喜歡史蒂芬霍金,在 ZEROBASE 遊樂場你可以駕駛霍金,讓他旋轉和跳躍。哦,我是世界上最聰明的人!讓我們乘坐時速 70 英里的飛行輪椅——由霍金本人駕駛!
這次金氏世界紀錄挑戰不僅證明了隱私運算技術可以實現大規模公眾參與,更展現了科技普惠與社會共識的重要性。這一點明確指出了隱私運算技術的未來不在於複雜的技術堆疊,而在於能否為一般使用者提供無門檻的參與途徑。
遊樂場入口: https://zerobase.pro/playground/index.html
未來目標:建構全球化的隱私運算基礎設施
隨著隱私運算逐步走出實驗室,它正悄悄重塑人類協作的底層秩序。未來,我們或許不再需要為每一次資料共享焦慮,因為保護隱私將成為系統預設的「基礎權利」;一個農民可以用隱私演算法預測氣候變化,一個社區可以在 DAO 中無中介地管理公共事務,一位身處偏遠地區的患者也能用可信 AI 安全共享病例、獲得全球最優解。
更遠的未來,或許我們也將見證隱私運算在量子時代為文明提供最後一道防線,成為數位社會可信運行的「安全恆星」。
回望今天,這場變革或許才剛開始。 但正如網路從協定走向世界,隱私運算也終將走向每個普通人。
真正值得銘記的,不是某一次科技的飛躍,而是我們共同選擇以何種方式,走向一個更自由、更安全、更可信的數位文明。
Refe rence
[ 1 ] Shamir A. How to share a secret. Commun ACM. 1979 Nov;22( 11): 612 – 3.
[ 2 ] Diffie W, Hellman M. New directions in cryptography. IEEE Trans Inf Theory. 1976 Nov;22( 6): 644 – 54.
[ 3 ] Calderbank. The rsa cryptosystem: history, algorithm, primes. Chicago: math uchicago edu [Internet].
[ 4 ] Yao AC. Protocols for secure computations. In: 23 rd Annual Symposium on Foundations of Computer Science (sfcs 1982). 1982. p. 160 – 4.
[ 5 ] Shannon CE. Communication theory of secrecy systems. The Bell System Technical Journal. 1949 Oct;28( 4): 656 – 715.
[ 6 ] Blakley. Safeguarding cryptographic keys. In: Managing Requirements Knowledge, International Workshop on. 1979. p. 313.
[ 7 ] Rabin MO. How To Exchange Secrets with Oblivious Transfer. Cryptology ePrint Archive [Internet]. 2005 [cited 2022 May 28 ];
[ 8 ] Rivest RL, Adleman L, Dertouzos ML. On data banks and privacy homomorphisms. Foundations of secure [Internet]. 1978;
[ 9 ] Goldwasser S, Micali S, Rackoff C. The knowledge complexity of interactive proof-systems [Internet]. Proceedings of the seventeenth annual ACM symposium on Theory of computing - STOC 85. 1985.
[ 10 ] Yao ACC. How to generate and exchange secrets. In: 27 th Annual Symposium on Foundations of Computer Science (sfcs 1986). 1986. p. 162 – 7.
[ 11 ] Goldreich O, Micali S, Wigderson A. How to Play ANY Mental Game. In: Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing. New York, NY, USA: ACM; 1987. p. 218 – 29. (STOC 87).
[ 12 ] Diffie W, Hellman M. New directions in cryptography. IEEE Trans Inf Theory. 1976 Nov;22( 6): 644 – 54.
[ 13 ] Paillier P. Public-Key Cryptosystem Based on Discrete Logarithm Residues. EUROCRYPT 1999 [Internet].
[ 14 ] Dwork C. Differential Privacy. In: Automata, Languages and Programming. Springer Berlin Heidelberg; 2006. p. 1 – 12.
[ 15 ] Hardware Working Group. ADVANCED TRUSTED ENVIRONMENT: OMTP TR 1 [Internet]. OMTP Limited; 2009.
[ 16 ] Gentry C. A fully homomorphic encryption scheme [Internet]. 2009. Available
[ 17 ] Wang S, Jiang X, Wu Y, Cui L, Cheng S, Ohno-Machado L. EXpectation Propagation LOgistic REgRession (EXPLORER): distributed privacy-preserving online model learning. J Biomed Inform.2013 Inform.4013.
[ 18 ] Gao D, Liu Y, Huang A, Ju C, Yu H, Yang Q. Privacy-preserving Heterogeneous Federated Transfer Learning. In: 2019 IEEE International Conference on Big Data (Big Data). 2019. p. 2552 – 9.
[ 19 ] Kone ny J, Brendan McMahan H, Yu FX, Richtárik P, Suresh AT, Bacon D. Federated Learning: Strategies for Improving Communication Efficiency [Internet]. arXiv [cs.LG]. 2016.
[ 20 ] Intel. Intel Architecture Instruction Set Extensions Programming Reference [Internet]. Intel; 2015.










