preamble
secondary title
In the current Bitcoin network or Ethereum network, there will be many transactions waiting to be packaged and confirmed in the entire network. This kind of transaction waiting for confirmation mechanism has greatly affected the user experience. Transaction congestion is an urgent problem that the entire industry needs to solve. In addition, due to the openness and transparency of the blockchain itself, once the address is marked, all our transactions will have no privacy at all. With the development of DeFi, in this dark forest of cryptocurrencies, the need for privacy protection has never been more urgent than it is now. When the DeFi building blocks were on the verge of collapsing, the clearly visible liquidation line and fixed-point liquidation on the chain became an important driving force behind the unstoppable price decline.
Table of contents:
Geeks and developers have been exploring for several years about the two major problems of network concurrent capacity and privacy. Zero-knowledge proof technology, with its own unique properties, is as important as transparency, decentralization and immutability to blockchain technology, and it brings solutions to expansion and privacy issues in its own right. This article will start from the definition and implementation of zero-knowledge proof, take many popular projects in the market as examples, discuss its exploration in the two fields of expansion and privacy protection, and consider the investment opportunities in it from the perspective of investment institutions.
Table of contents:
Zero-knowledge proofs and privacy
Zero Knowledge Proof and Scaling
Zero-knowledge proofs and privacy
Investment direction of zero-knowledge proof
Investment direction of zero-knowledge proof
secondary title"Definition of Zero Knowledge Proof"People tend to believe what they see and hear in the process of life interaction, but for valuable information, or knowledge, its owner will want to convince others that he is right without revealing the core secrets. Knowledge is owned. In order to solve such needs, zero-knowledge proofs came into being. Switching to a more academic expression, zero-knowledge proof is that the two parties
Proof and verification, where the owner of the knowledge is also the prover, and the other party is the verifier.
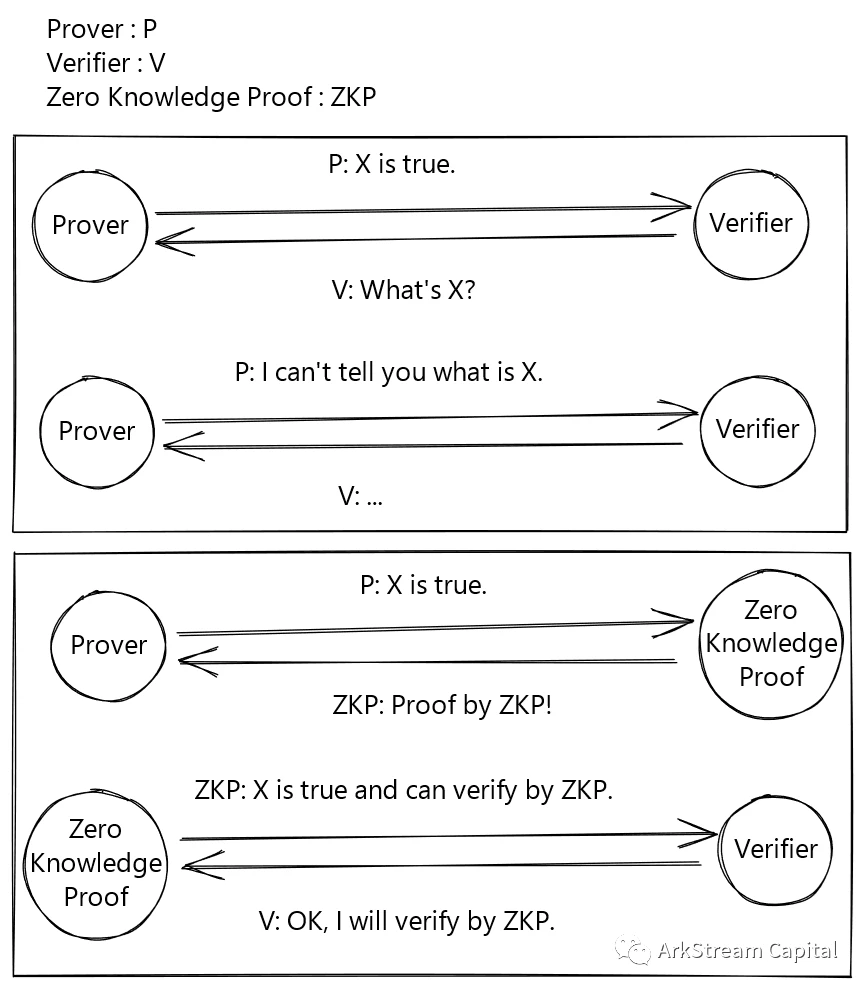
Figure 1: Proof without ZKP and with ZKP
We use a sketch to intuitively explain what zero-knowledge proofs can achieve.
image descriptionFrom this picture, we can extract three properties of zero-knowledge proof:"Completeness (Complete)": honest proof party, right
knowledge is trueThe proof of this assertion will definitely convince the verifier.
Rationality (Sound): The prover cannot prove knowledge is false to knowledge is true.
: Throughout the proof, the verifier will not obtain other secrets related to knowledge except for the assertion that knowledge is true.
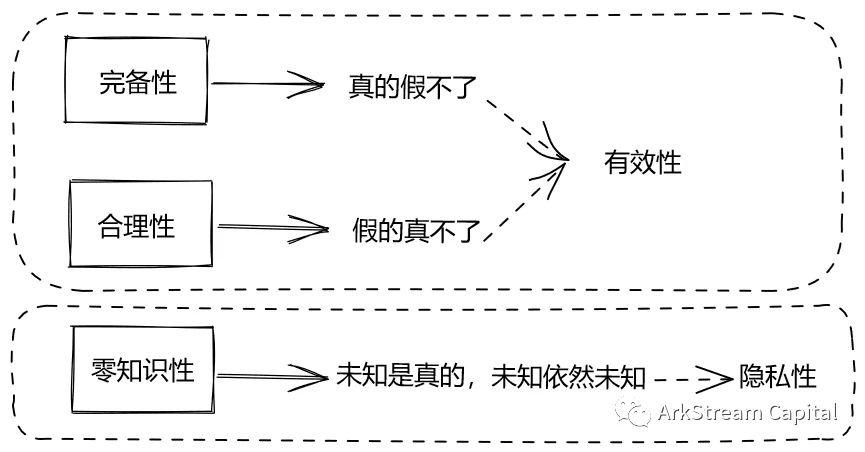
To put these three properties in plain language, they are: what is true cannot be false; what is false cannot be true; the unknown is true, and the unknown remains unknown. The third property is a more popular way of saying, I said what is true, you have verified what is true, but you dont know what is what.
image description
Figure 2: Zero-knowledge proof three properties and two characteristics
The first two properties are easier to understand and pay attention to than the third property, while the third property is very easy to be confused and ignored.
Lets talk about it with more specific examples. For example, we all believe that Satoshi Nakamoto must exist in the world, otherwise, Bitcoin would never have appeared. However, after so many years, we dont know whether Satoshi Nakamoto is alive in the world. If Satoshi Nakamoto is still alive, and he wants to tell the world that he is still alive. Then, Satoshi Nakamoto can use the zero-knowledge proof to convey I am still alive to the world. At this time, the world knows this information according to the zero-knowledge proof verification, but it will not know whether Satoshi Nakamoto has used the private key or whether he has logged into the world. BitcoinTalk account self-certification, etc. Another scenario is that when Satoshi Nakamoto invented Bitcoin, the genesis address owned the first bitcoin. When this address uses the corresponding private key for activities, it can also convey the information that Satoshi Nakamoto is still alive. But this no longer satisfies zero-knowledge, because the world knows that Satoshi Nakamoto is still alive because of his private key activity.
Simply put, zero-knowledge proof can not only guarantee the privacy of knowledge, but also guarantee the validity of knowledge. These two points directly determine the two major application scenarios of zero-knowledge proof in the encrypted world: privacy and expansion. Of course, there will be more subdivided applications in privacy scenarios, such as private payment, anonymous voting and even private public chains, etc., which can also be generally understood as asset payment privacy and logical general privacy. As for the expansion scenario, the completeness and rationality of the zero-knowledge proof is used, as well as other technical means.
secondary titleImplementation of zero-knowledge proof
Zero-knowledge proofs are invented and implemented using a lot of mathematical and cryptography knowledge.
In the implementation of the entire proof, according to whether it is interactive or not, it can be divided into interactive proof and non-interactive proof. Interactive proof is a proof process that requires the prover and the verifier to alternate in a certain order and rules, and then complete the proof through random probability. Non-interactive proof means that the prover calculates and submits all proof materials at one time according to the proof rules or proof process, and then the verifier can directly use these proof materials for verification. In an extreme understanding, non-interactive proof is to compress multiple steps of interactive proof into one interaction. In addition, non-interactive proof can be seen as splitting the entire implementation into a proof process and a verification process.
Below, we simulate the difference between interactive and non-interactive proofs with two different scenarios.
Simplify scenario 1, assuming that Satoshi Nakamoto’s creation private key reappears in the world, now, it is necessary to prove that this private key is still active.
The process of interactive proof:
1. The verifier shouts the genesis private key to the prover, and you write a sentence after a certain block height: Hello World.
2. The genesis private key certifier waits for a certain block height as required, and then sends a message to the entire network: Hello World.
3. The verifier verifies in the network whether the genesis private key leaves a message after a certain block height as required: Hello World.
4. Repeat steps 1, 2, and 3. When the number of times reaches a certain level, it can be determined from the perspective of probability that the private key is basically active.
The process of non-interactive proof:
1. A certain device/simulator/Turing machine generates a shared, random string xyz, and then makes this string public, and requires the genesis private key prover to send to the whole network in the form of xyz, Hello World. message.
2. The genesis private key prover, according to the rules of the device/simulator/Turing machine, uses this string xyz, adds his own Hello World, and leaves a message to the whole network: xyz, Hello World.
3. The verifier holds the string xyz, and after seeing the message of the genesis private key, directly determines that the private key is active.
Simplify scenario 2, assuming that Zhang San understands the Gaussian algorithm and Li Si does not.
The process of interactive proof:
1. Li Si calls Zhang San, and calculates 1+2+3+...+8887+8888 within 30 seconds.
2. Zhang San took the Gaussian algorithm, calculated the result in 30 seconds, and told Li Si.
3. Li Si uses his simplest addition to check whether the result is correct.
4. Repeat steps 1, 2, and 3. When the number of times reaches a certain level, it can be determined from the perspective of probability that Zhang San understands the Gaussian algorithm.
The process of non-interactive proof:
1. A device/simulator/Turing machine generates a shared random integer x.
2. Zhang San uses the Gaussian algorithm to directly calculate the result of 1+2+3+...+(x-1)+x.
3. Li Si uses his simplest addition to check whether the result is correct. If it is correct, Zhang San understands the Gaussian algorithm.
Through the above example, we can find that non-interactive proofs have obvious advantages over interactive proofs: 1. It does not depend on a specific interactive verifier, and is an excellent solution for one prover to N verifiers; 2. Not limited to the moment of interaction, it can be done at any time. However, we also noticed that there are more simulators/Turing machines in the non-interactive proof!In order to realize the core functions of the simulator/Turing machine for non-interactive proofs, the current technical solutions probably include:andRandom oracle (Random Oracle)and
Common Reference String (Common Reference String, CRS)
, and where public reference strings are widely used schemes. We believe that there is not much essential difference between a random oracle and a public reference string. The public reference string CRS must be generated by a trusted third party, and then shared with the prover and verifier. Here, the generation of CRS must be guaranteed to be random and credible. Therefore, the link of generating CRS is also called trusted setup, Trusted Setup.We can use God as a metaphor for a simulator/Turing machine. God is public. It can not only help the prover hide knowledge, assist the prover to complete the proof, but also identify whether the prover has falsified knowledge, and assist the verifier to verify smoothly. God is perfect, but people need to create God after all. The process of creating God can be corresponded to: believable setting. In addition, gods have applicability, and they are not necessarily universal, just like Jesus is the god of the West, and Tathagata is the god of the East (applicability of credible settings). If you think about it more deeply, God may also be unreliable. (Security that can be newly set)
As for QAP/QSP, Boolean circuits and arithmetic circuits, we simply and roughly classify them as specific steps in the non-interactive proof process. There are tens of thousands of mathematical proof questions in the world. When solving a proof, you need to write the corresponding problem-solving steps. Similarly, for zero-knowledge proofs under different knowledge, circuits also need to be specially written. Of course, there are also certain kinds of proofs of knowledge that can simplify the process of writing by sharing the circuit framework. For different mathematical proof questions, we have to write a separate answering step (dedicated circuit), and for a certain type of mathematical proof question, we can write a general answering step (general circuit), and even, for a class of questions, we can directly Citing already written answer steps/conclusions for another type of topic. (Composability/interactivity of circuits).

Talk about the position of the circuit along the previous mathematical proof questions
image description
Figure 3: Circuit Analogy
As for other concepts or terms, such as first-order constraint system R1CS, NP problem, polynomial, polynomial knowledge, factorization, fuzzy calculation, information, knowledge, circuit satisfiability, complete security, semantic security, indistinguishability, mapping , homomorphism, finite field, cyclic group, Fiat-Shamir transformation, ECDSA signature... Because it involves too many concepts and mathematical calculations, unless you are an expert in mathematics and cryptography, it is not recommended to spend too much brainpower and energy on this aspect. The key information we only need to know is: different zero-knowledge proof implementation schemes lie in the introduction of trusted settings, the applicability of trusted settings, and the ease of writing circuits.
For different zero-knowledge proof implementation schemes, we can use the time and space overhead of the prover and verifier, as well as security, these five dimensions are used to determine the pros and cons of the implementation.
The time overhead of the prover: that is, the calculation time, which determines the speed of the proof;
The time overhead of the verifier: that is, the verification time;
The space overhead of the prover and the verifier: there is a concept of proof size, which determines the storage space usage requirements, and is also often referred to as simplicity;
Security: Since some protocols need to introduce trusted settings, the corresponding implementation schemes will rely on new settings in terms of security. In addition, there are also differences in applicability of trusted settings, that is, permanent and one-time.
The different implementation schemes finally divided into two factions of zero-knowledge proof protocols: zk-SNARK zero-knowledge concise non-interactive knowledge argumentation and zk-STARK zero-knowledge scalable transparent knowledge argumentation.
zk-STARK: Zero-Knowledge Scalable Transparent Argument of Knowledge. Non-interactive proofs, no need for trusted settings, anti-quantum computing, high proof size overhead. The Starkware team invented and proposed that there are some dedicated projects in use, dYdX (recently announced the migration to Cosmos), Immutable, and Deversifi.
Referring to the impossible triangle of the blockchain, the implementation of zero-knowledge proof can be said to be an imperfect triangle. Although all implementations can achieve completeness, rationality, and zero-knowledge at the same time, because of the requirements of application scenarios, they are all There is a certain trade-off. Or more obviously, when focusing on completeness and rationality, the implementation of zero-knowledge will be weakened, and may even be ignored (Layer 2 expansion). In addition, zero-knowledge proof itself does not have the attribute of decentralization. If there is a requirement in this regard, it needs to be combined with a decentralized design (even more difficult).
Virtual Machine for Zero-Knowledge Proof
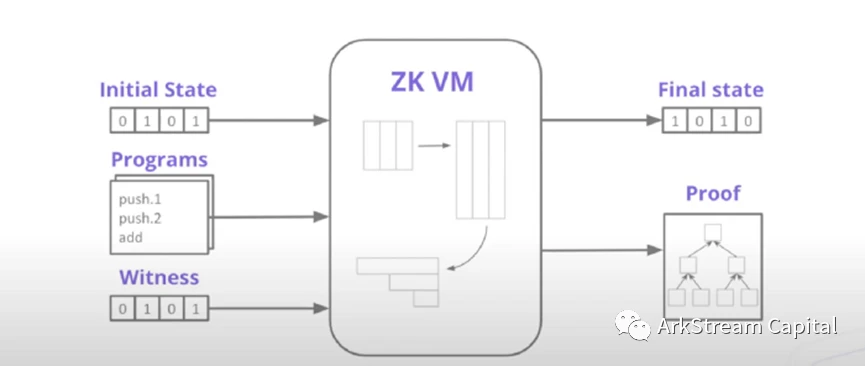
Figure 4:Polygon Miden Deep Dive zkVM
After discussing the different implementation schemes, we next discuss the key to the implementation of the scheme. Todays Internet applications and products are programs implemented in high-level programming languages (C++, Java, Rust, Solidity...). The virtual machine/interpreter is a black box for program execution, which can convert the program into a language that the machine can recognize and understand, and then run the program instead of the machine. If there is no virtual machine for zero-knowledge proof, when we use zero-knowledge proof technology to write a program, we need to write a corresponding implementation circuit for the program. Writing, testing, and production use of such circuits is very difficult and inefficient. To this end, a zero-knowledge proof virtual machine (zkVM) that can generate proofs for program generation, submission and verification, is necessary to make the use of zero-knowledge technology more widespread and efficient. As for whether the high-level programming language adopted by zkVM is C++, Java, or a specially designed high-level circuit programming language (Cairo of Stareware, Zinc of zkSync), these depend on the design and capabilities of zkVM. It should be emphasized that zkVM does not have a rigid requirement to use the blockchain.image description。
For zkVM, it is very important to be able to support programs universally. If only certain types of programs can be virtualized, the versatility of this zkVM will be greatly reduced. In addition to generality,
Simplicity, recursive usability, composability, and ease of use are other metrics to consider
Here are mainly examples to illustrate recursive availability:
1+2=3,3+3=6,6+4=10,...,4950+100=5050
Question: Assuming that the computer only supports two-digit addition, but does not support multi-digit addition and multiplication, calculate 1+2+3+...+99+100?
Non-recursive solution:
1+2+3+...+99+100
A total of 99 additions are performed. (The concept of iteration is not introduced here, those who are interested can search and learn by themselves)The recursive version solves:。
Calculate the sum of 1 and (2+3+...+99+100). As for the calculation of (2+3+...+99+100), you can reuse this method to solve it, that is, (2+3 +...+99+100) is converted to calculate 2 and (3+...+99+100), and so on to meet the restriction of two-digit addition, that is, 99+100 = 199, and then use 199 to
End the recursion and calculate the result
Recursive availability can directly reuse the solution to the problem when solving the problem. This can greatly simplify the solution to practical problems.
Ideals are beautiful, but reality is always skinny, even cruel. When Ethereum was founded, it did not consider the introduction of zero-knowledge proof. Therefore, if Ethereum is directly zero-knowledge proof, the biggest problem will be that most of the components of the Ethereum protocol will lead to a large number of zero-knowledge proof calculations. , which does not take advantage of zero-knowledge proofs in essence. Of course, the Ethereum protocol itself can be updated iteratively with the development of time and technology. Like the epoch-making consensus mechanism change from PoW to PoS, the zero-knowledge proof of the Ethereum protocol may be achieved through Ethereum upgrades in the future.
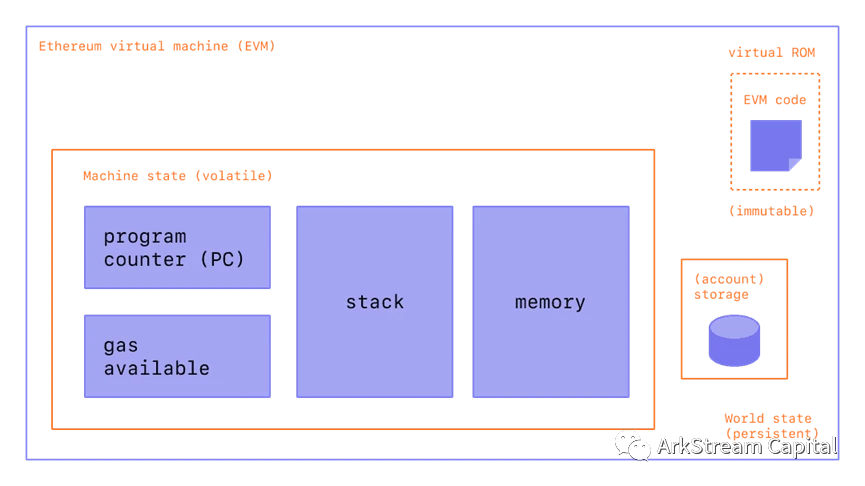
Figure 5: ETHEREUM VIRTUAL MACHINE (EVM)
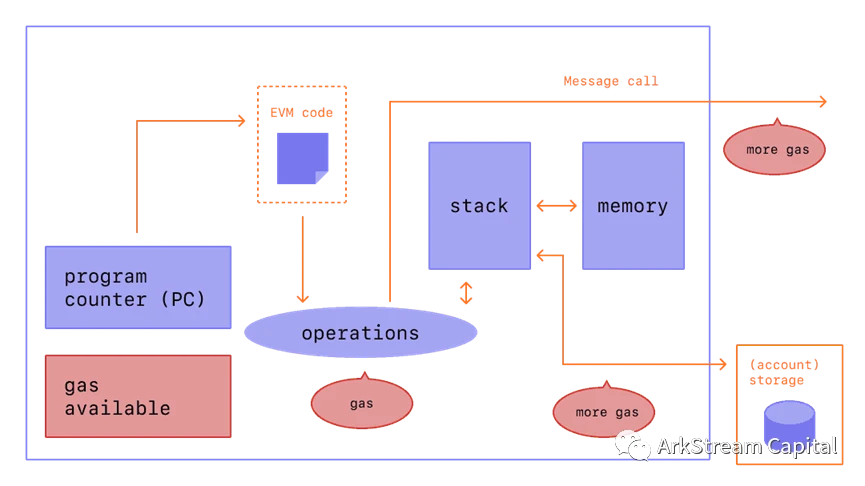
Figure 6: ETHEREUM VIRTUAL MACHINE (EVM)
image description
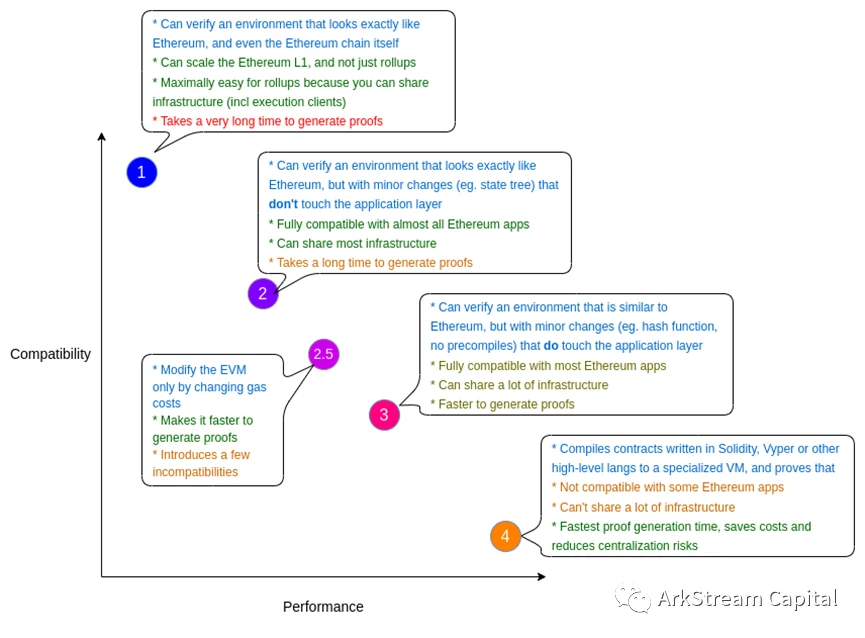
Figure 7: The different types of ZK-EVMs

Figure 8
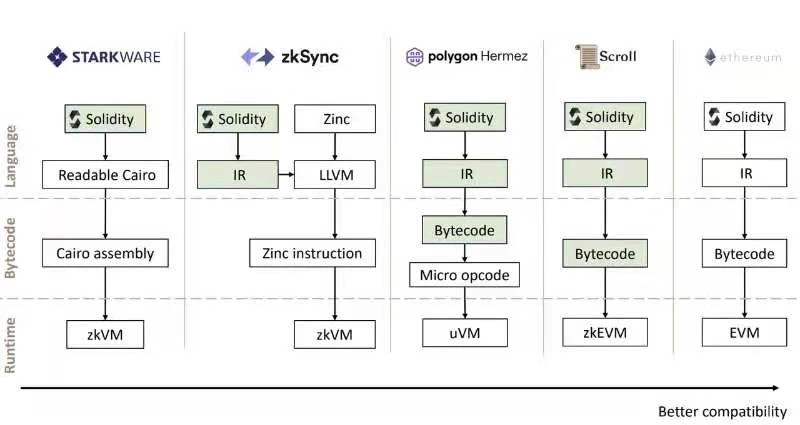
Figure 9
image description
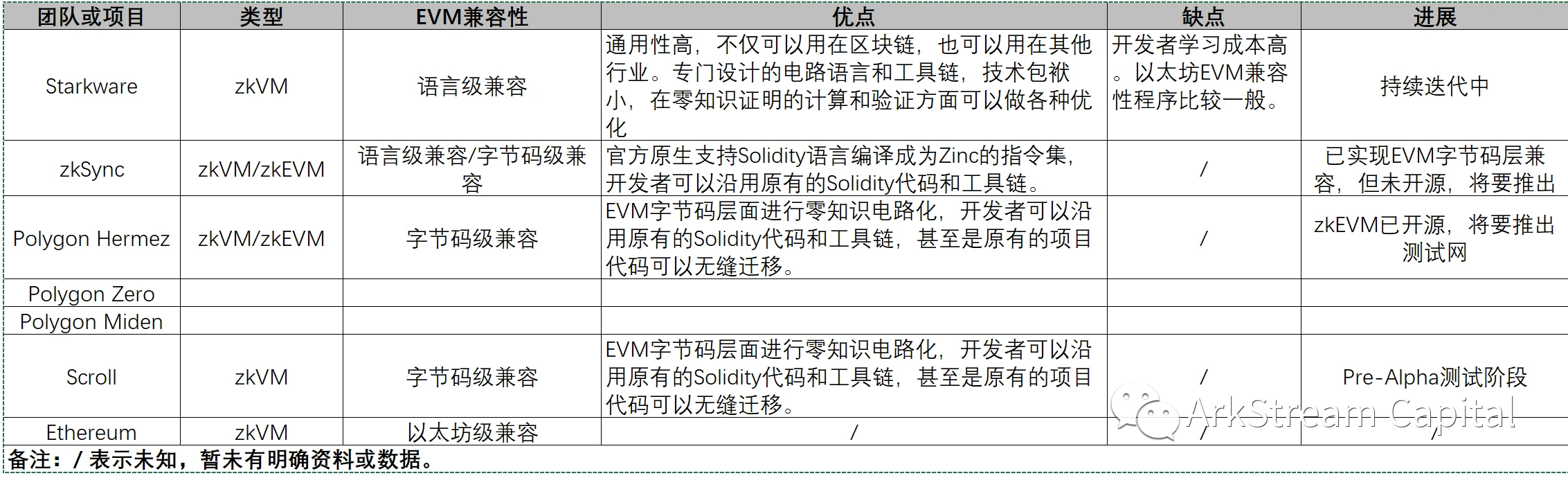
Figure 10
image description
References:
The research and implementation of zkVM and zkEVM face different implementation problems, and there is no sequence dependence, so they can be promoted simultaneously and in parallel. For specific design challenges and solutions, you can refer to the materials and documents of each project. Different projects must have their own considerations for the choice of zkVM/zkEVM. At present, most of them will tend to give priority to the zkEVM road. After all, the just-needed scenarios for Ethereum expansion have always existed. In addition, the ultimate ZK goal of Ethereum itself is to be fully compatible. Thinking about it this way, projects based on zkEVM research and development may evolve into a variety of Ethereum light node clients in the future. As for zkVM, we can only say that the blockchain must be its partner, but its distant dreams are not limited to the blockchain.
[2] https://mp.weixin.qq.com/s/808jMXvIUqB973aVHrAzGQReferences:
[1] https://github.com/sec-bit/learning-zkp/blob/master/zkp-resource-list.md Summary of zero-knowledge proof learning resources
Foresight Ventures: Interpretation of zk, zkVM, zkEVM and their future
[3] https://www.odaily.news/post/5178462Scroll research: zkEVM design challenges and solutions
[6] https://ethereum.org/en/developers/docs/evm/Ethereum Virtual Machine










