전문
보조 제목
현재 비트코인 네트워크나 이더리움 네트워크에는 전체 네트워크에서 패키징되고 확인되기를 기다리는 많은 트랜잭션이 있을 것입니다. 이러한 종류의 거래 확인 대기 메커니즘은 사용자 경험에 큰 영향을 미쳤으며 거래 혼잡은 전체 업계가 해결해야 할 시급한 문제입니다. 또한 블록체인 자체의 개방성과 투명성으로 인해 주소가 표시되면 모든 거래에 프라이버시가 전혀 없습니다. DeFi의 개발과 함께 이 어두운 암호 화폐의 숲에서 개인 정보 보호의 필요성이 지금보다 더 시급한 적은 없었습니다. DeFi 빌딩 블록이 붕괴 직전에 있을 때 명확하게 보이는 청산 라인과 체인의 고정 소수점 청산은 멈출 수 없는 가격 하락의 중요한 원동력이 되었습니다.
목차:
괴짜와 개발자는 네트워크 동시 용량과 프라이버시라는 두 가지 주요 문제에 대해 수년 동안 탐구해 왔습니다. 고유한 속성을 지닌 영지식 증명 기술은 블록체인 기술에 대한 투명성, 탈중앙화, 불변성만큼 중요하며, 그 자체로 확장성 및 개인 정보 보호 문제에 대한 솔루션을 제공합니다. 이 기사는 영지식 증명의 정의 및 구현에서 시작하여 시장에서 인기 있는 많은 프로젝트를 예로 들어 확장 및 개인 정보 보호의 두 가지 분야에 대한 탐색을 논의하고 투자의 관점에서 투자 기회를 고려합니다. 기관.
목차:
영지식 증명 및 프라이버시
제로 지식 증명 및 확장
영지식 증명 및 프라이버시
영지식증명의 투자방향
영지식증명의 투자방향
보조 제목"제로 지식 증명의 정의"사람들은 삶의 교류 과정에서 보고 듣는 것을 믿는 경향이 있지만, 가치 있는 정보나 지식에 대해서는 그 소유자가 핵심 비밀을 밝히지 않고 자신이 옳다고 다른 사람을 납득시키려 할 것입니다. 이러한 요구를 해결하기 위해 영지식 증명이 등장했습니다. 보다 학술적인 표현으로 전환하면 영지식 증명은 두 당사자가
지식의 소유자가 증명자이기도 하고 상대방이 검증자이기도 한 증명 및 검증.
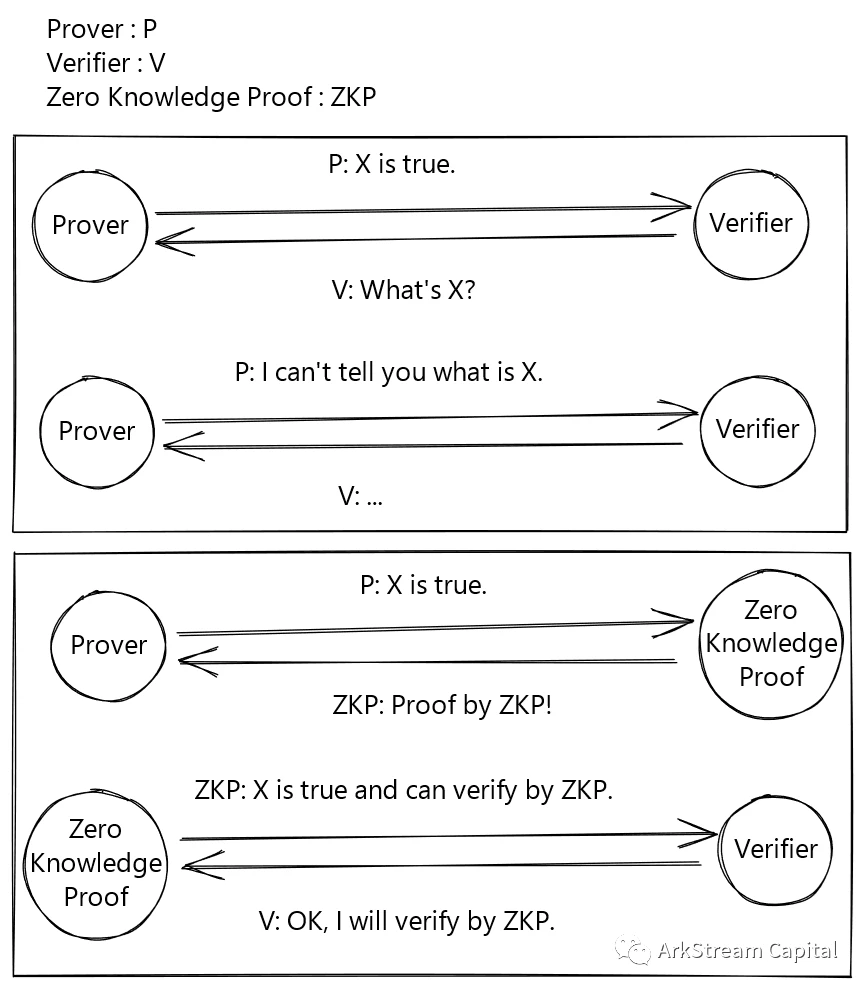
Figure 1: Proof without ZKP and with ZKP
우리는 영지식 증명이 달성할 수 있는 것을 직관적으로 설명하기 위해 스케치를 사용합니다.
이미지 설명이 그림에서 영지식 증명의 세 가지 속성을 추출할 수 있습니다."완결성(Complete)": 정직증명당, 맞다
지식은 사실이다이 주장의 증명은 확실히 검증자를 설득할 것입니다.
합리성(사운드): 증명자는 지식이 거짓을 지식이 참으로 증명할 수 없습니다.
: 증명하는 동안 검증자는 지식은 참이라는 주장을 제외하고는 지식과 관련된 다른 비밀을 얻지 않습니다.
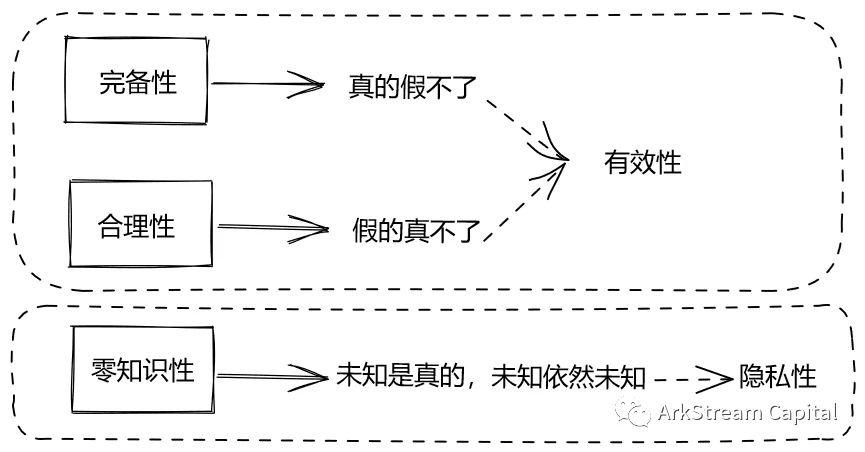
이 세 가지 속성을 평이하게 표현하면 참인 것은 거짓일 수 없고, 거짓인 것은 참일 수 없으며, 알려지지 않은 것은 참이고, 알려지지 않은 것은 여전히 알려지지 않은 것입니다. 세 번째 속성은 좀 더 대중적으로 말하는 방식입니다. 내가 무엇이 사실인지라고 말했지만 귀하는 무엇이 사실인지를 확인했지만 무엇이 무엇인지 모릅니다.
이미지 설명
그림 2: 영지식 증명의 세 가지 속성과 두 가지 특성
처음 두 속성은 세 번째 속성보다 이해하기 쉽고 주의를 기울이기 쉬운 반면 세 번째 속성은 혼동하고 무시하기가 매우 쉽습니다.
좀 더 구체적인 예를 들어 이야기해 보겠습니다. 예를 들어, 우리 모두는 Satoshi Nakamoto가 세상에 존재해야 한다고 믿습니다. 그렇지 않으면 Bitcoin이 나타나지 않았을 것입니다. 세계. 사토시 나카모토가 아직 살아 있고, 그가 아직 살아 있다는 것을 세상에 알리고 싶다면. 그러면 사토시 나카모토는 영지식 증명을 이용해 나는 아직 살아있다는 세상에 전할 수 있다. 개인 키를 사용했는지 또는 세계에 로그인했는지 여부 BitcoinTalk 계정 자체 인증 등 또 다른 시나리오는 Satoshi Nakamoto가 비트코인을 발명했을 때 최초의 비트코인을 소유한 제네시스 주소가 해당 개인 키를 활동에 사용하면 Satoshi Nakamoto가 아직 살아 있다는 정보도 전달할 수 있지만 더 이상 영지식을 만족시키지 못한다는 것입니다. , 사토시 나카모토가 개인 키 활동으로 아직 살아 있다는 것을 세상이 알고 있기 때문입니다.
간단히 말해서 영지식 증명은 지식의 프라이버시를 보장할 뿐만 아니라 지식의 유효성도 보장할 수 있습니다. 이 두 지점은 암호화된 세계에서 영지식 증명의 두 가지 주요 응용 시나리오인 프라이버시와 확장을 직접 결정합니다. 물론 프라이빗 지불, 익명 투표, 심지어 프라이빗 퍼블릭 체인 등과 같이 일반적으로 자산 지불 프라이버시 및 논리적 일반 프라이버시로 이해될 수 있는 프라이버시 시나리오에서 더 세분화된 애플리케이션이 있을 것입니다. 확장 시나리오는 영지식 증명의 완전성과 합리성과 기타 기술적 수단을 사용합니다.
보조 제목영지식 증명 구현
영지식 증명은 많은 수학 및 암호 지식을 사용하여 발명되고 구현됩니다.
전체 증명의 구현에서 대화식인지 아닌지에 따라 대화식 증명과 비대화식 증명으로 나눌 수 있습니다. 대화식 증명은 증명자와 검증자가 특정 순서와 규칙으로 번갈아 가며 무작위 확률을 통해 증명을 완료하는 증명 프로세스입니다. 비대화형 증명은 증명자가 증명 규칙 또는 증명 프로세스에 따라 한 번에 모든 증명 자료를 계산하고 제출한 다음 검증자가 이러한 증명 자료를 직접 검증에 사용할 수 있음을 의미합니다. 극단적인 이해에서 비대화형 증명은 여러 단계의 대화형 증명을 하나의 상호 작용으로 압축하는 것입니다. 또한 비대화형 증명은 전체 구현을 증명 프로세스와 검증 프로세스로 나누는 것으로 볼 수 있습니다.
아래에서는 두 가지 시나리오를 사용하여 대화식 증명과 비대화식 증명의 차이를 시뮬레이션합니다.
시나리오 1을 단순화하여 Satoshi Nakamoto의 생성 개인 키가 세상에 다시 나타난다고 가정하면 이제 이 개인 키가 여전히 활성 상태임을 증명해야 합니다.
대화식 증명 프로세스:
1. 검증자는 증명자에게 제네시스 개인 키를 외치고 특정 블록 높이 이후에 Hello World라는 문장을 작성합니다.
2. 제네시스 개인 키 인증자는 필요에 따라 특정 블록 높이를 기다린 다음 전체 네트워크에 Hello World라는 메시지를 보냅니다.
3. 검증자는 필요에 따라 특정 블록 높이 이후 제네시스 개인 키가 메시지를 남기는지 여부를 네트워크에서 확인합니다: Hello World.
4. 1, 2, 3단계를 반복한다. 그 횟수가 일정 수준에 도달하면 기본적으로 개인키가 활성 상태일 확률의 관점에서 판단할 수 있다.
비대화형 증명 프로세스:
1. 특정 장치/시뮬레이터/튜링 머신은 임의의 공유 문자열 xyz를 생성한 다음 이 문자열을 공개하고 xyz, Hello World 형식으로 전체 네트워크에 전송하기 위해 제네시스 개인 키 증명자를 요구합니다. .
2. 장치/시뮬레이터/튜링 머신의 규칙에 따라 제네시스 개인 키 증명자는 이 문자열 xyz를 사용하고 자신의 Hello World를 추가하고 전체 네트워크에 xyz, Hello World라는 메시지를 남깁니다.
3. 검증자는 문자열 xyz를 보유하고 제네시스 개인 키의 메시지를 확인한 후 개인 키가 활성 상태인지 직접 결정합니다.
Zhang San은 가우시안 알고리즘을 이해하고 Li Si는 이해하지 못한다고 가정하고 시나리오 2를 단순화합니다.
대화식 증명 프로세스:
1. Li Si는 Zhang San에게 전화를 걸어 30초 이내에 1+2+3+...+8887+8888을 계산합니다.
2. Zhang San은 가우스 알고리즘을 사용하여 30초 안에 결과를 계산하고 Li Si에게 말했습니다.
3. Li Si는 결과가 올바른지 확인하기 위해 가장 간단한 덧셈을 사용합니다.
4. 1, 2, 3단계를 반복한다. 횟수가 일정 수준에 도달하면 장산이 가우시안 알고리즘을 이해하는 확률의 관점에서 판단할 수 있다.
비대화형 증명 프로세스:
1. 장치/시뮬레이터/튜링 기계는 공유된 임의의 정수 x를 생성합니다.
2. Zhang San은 가우스 알고리즘을 사용하여 1+2+3+...+(x-1)+x의 결과를 직접 계산합니다.
3. Li Si는 그의 가장 간단한 덧셈을 사용하여 결과가 올바른지 확인하고, 맞으면 Zhang San은 가우시안 알고리즘을 이해합니다.
위의 예를 통해 비대화형 증명이 대화형 증명에 비해 분명한 이점이 있음을 알 수 있습니다. 상호 작용의 순간, 그것은 언제든지 할 수 있습니다. 그러나 우리는 또한 비대화형 증명에 더 많은 시뮬레이터/튜링 기계가 있음을 발견했습니다!비대화형 증명을 위한 시뮬레이터/튜링 머신의 핵심 기능을 실현하기 위한 현재 기술 솔루션에는 다음이 포함될 수 있습니다.그리고랜덤 오라클(랜덤 오라클)그리고
공통 참조 문자열(Common Reference String, CRS)
, 공용 참조 문자열이 널리 사용되는 체계입니다. 우리는 무작위 오라클과 공개 참조 문자열 사이에 본질적인 차이가 크지 않다고 생각합니다. 공개 참조 문자열 CRS는 신뢰할 수 있는 제3자가 생성한 다음 증명자 및 검증자와 공유해야 합니다. 여기서 CRS 생성은 임의적이고 신뢰할 수 있어야 하므로 CRS 생성 링크를 신뢰 설정(trusted setup), 신뢰 설정(Trusted Setup)이라고도 한다.우리는 신을 시뮬레이터/튜링 기계에 대한 은유로 사용할 수 있습니다. 신은 공개적입니다. 증명자가 지식을 숨기고 증명자가 증명을 완료하도록 도울 수 있을 뿐만 아니라 증명자가 지식을 위조했는지 여부를 식별하고 검증자를 도울 수 있습니다. 원활하게 확인합니다. 신은 완전하지만 인간은 결국 신을 창조해야 한다 신을 창조하는 과정은 믿을 수 있는 설정에 해당된다. 또한 신은 적용 가능성이 있으며, 예수가 서양의 신이고 Tathagata가 동양의 신인 것처럼 반드시 보편적인 것은 아닙니다(신뢰할 수 있는 설정의 적용 가능성). 더 깊이 생각해보면 하나님도 믿을 수 없는 분일 수 있습니다. (새로 설정할 수 있는 보안)
QAP/QSP, 부울 회로 및 산술 회로의 경우 비대화식 증명 프로세스의 특정 단계로 간단하고 대략적으로 분류합니다. 세상에는 수만 개의 수학적 증명 문제가 있으며, 증명을 풀 때 해당 문제 해결 단계를 작성해야 합니다. 마찬가지로 서로 다른 지식 하의 영지식 증명을 위해 회로도 특별히 작성해야 합니다. 물론 회로 프레임워크를 공유하여 작성 프로세스를 단순화할 수 있는 특정 종류의 지식 증명도 있습니다. 다양한 수학적 증명 질문에 대해 별도의 답변 단계(전용 회로)를 작성해야 하며 특정 유형의 수학 증명 질문에 대해 일반 응답 단계(일반 회로)를 작성할 수 있으며, 심지어 질문 클래스에 대해 다른 유형의 주제에 대해 이미 작성된 답변 단계/결론을 직접 인용할 수 있습니다. (회로의 구성성/상호작용성).

이전 수학적 증명 질문에 따라 회로의 위치에 대해 이야기하십시오.
이미지 설명
그림 3: 회로 비유
1차 제약 시스템 R1CS, NP 문제, 다항식, 다항식 지식, 분해, 퍼지 계산, 정보, 지식, 회로 만족, 완전 보안, 의미 보안, 비구별 가능성, 매핑, 동형, 유한 필드와 같은 다른 개념이나 용어에 대해서는 , 순환 그룹, Fiat-Shamir 변환, ECDSA 서명... 너무 많은 개념과 수학적 계산이 포함되기 때문에 수학과 암호학의 전문가가 아닌 한 이 측면에 너무 많은 두뇌와 에너지를 소비하는 것은 권장되지 않습니다. 우리가 알아야 할 핵심 정보는 신뢰할 수 있는 설정의 도입, 신뢰할 수 있는 설정의 적용 가능성 및 회로 작성의 용이성에 있는 다양한 영지식 증명 구현 체계입니다.
다양한 영지식 증명 구현 체계의 경우 증명자와 검증자의 시간 및 공간 오버헤드와 보안을 사용할 수 있습니다. 이러한 5가지 차원은 구현의 장단점을 결정하는 데 사용됩니다.
증명자의 시간 오버헤드: 즉, 증명 속도를 결정하는 계산 시간입니다.
검증자의 시간 오버헤드: 즉, 검증 시간;
증명자와 검증자의 공간 오버헤드: 저장 공간 사용 요구 사항을 결정하고 종종 단순성이라고도 하는 증명 크기의 개념이 있습니다.
보안: 일부 프로토콜은 신뢰할 수 있는 설정을 도입해야 하므로 해당 구현 체계는 보안 측면에서 새로운 설정에 의존합니다. 또한 신뢰할 수 있는 설정의 적용 여부, 즉 영구와 일회성에도 차이가 있습니다.
서로 다른 구현 체계는 최종적으로 영지식 증명 프로토콜의 두 가지 파벌인 zk-SNARK 영지식 간결한 비대화형 지식 논증과 zk-STARK 영지식 확장 가능한 투명한 지식 논증으로 나뉩니다.
zk-STARK: 영지식 확장 가능 투명한 지식 인수. 비대화형 증명, 신뢰할 수 있는 설정 필요 없음, 반양자 컴퓨팅, 높은 증명 크기 오버헤드. Starkware 팀은 dYdX(최근 Cosmos로의 마이그레이션 발표), Immutable 및 Deversifi와 같은 일부 전용 프로젝트를 발명하고 사용 중이라고 제안했습니다.
블록체인의 불가능한 삼각형을 참조하여 영지식 증명의 구현은 불완전한 삼각형이라고 할 수 있습니다.응용 시나리오의 요구 사항으로 인해 모든 구현이 완전성, 합리성 및 영지식을 동시에 달성할 수 있지만 , 그들은 모두 특정 트레이드 오프가 있습니다. 또는 더 명백하게는 완전성과 합리성에 초점을 맞추면 영지식의 구현이 약화되고 심지어 무시될 수도 있습니다(계층 2 확장). 또한 영지식 증명 자체는 탈중앙화의 속성을 가지고 있지 않으며, 이에 대한 요구사항이 있다면 탈중앙화 설계와 결합해야 합니다(더 어렵습니다).
영지식 증명을 위한 가상 머신
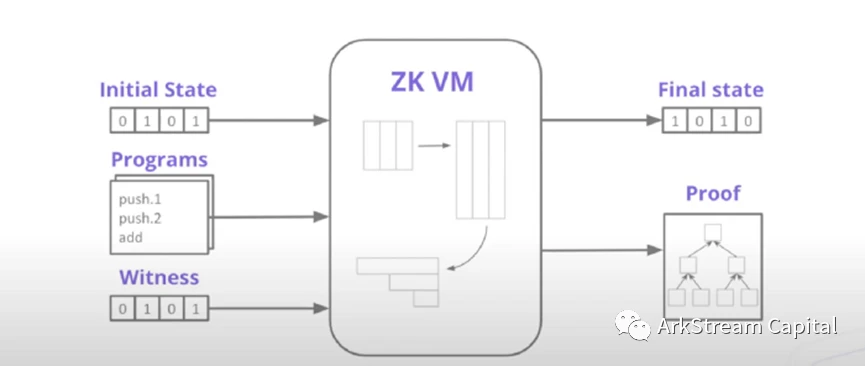
Figure 4:Polygon Miden Deep Dive zkVM
다양한 구현 체계를 논의한 후 다음으로 체계 구현의 핵심에 대해 논의합니다. 오늘날의 인터넷 응용 프로그램 및 제품은 고급 프로그래밍 언어(C++, Java, Rust, Solidity...)로 구현된 프로그램입니다. 가상머신/통역사는 프로그램 실행을 위한 블랙박스로서, 프로그램을 기계가 인식하고 이해할 수 있는 언어로 변환한 후 기계 대신 프로그램을 실행할 수 있다. 영지식 증명을 위한 가상 머신이 없다면 영지식 증명 기술을 사용하여 프로그램을 작성할 때 프로그램에 해당하는 구현 회로를 작성해야 합니다. 이러한 회로의 쓰기, 테스트 및 프로덕션 사용은 매우 어렵고 비효율적입니다. 이를 위해 프로그램 생성, 제출 및 검증을 위한 증명을 생성할 수 있는 영지식 증명 가상 머신(zkVM)이 영지식 기술을 보다 광범위하고 효율적으로 사용하기 위해 필요합니다. zkVM이 채택한 고급 프로그래밍 언어가 C++, Java 또는 특별히 설계된 고급 회로 프로그래밍 언어(Stareware의 Cairo, zkSync의 Zinc)인지 여부는 zkVM의 설계 및 기능에 따라 다릅니다. zkVM은 블록체인을 사용하기 위한 엄격한 요구 사항이 없다는 점을 강조해야 합니다.이미지 설명。
zkVM의 경우 프로그램을 보편적으로 지원할 수 있는 것이 매우 중요하며 특정 유형의 프로그램만 가상화할 수 있다면 이 zkVM의 범용성은 크게 줄어들 것입니다. 일반성 외에도,
단순성, 재귀적 유용성, 구성 가능성 및 사용 용이성은 고려해야 할 다른 메트릭입니다.
다음은 재귀적 가용성을 설명하는 주요 예입니다.
1+2=3,3+3=6,6+4=10,...,4950+100=5050
질문: 컴퓨터가 두 자리 덧셈만 지원하고 여러 자리 덧셈과 곱셈을 지원하지 않는다고 가정하면 1+2+3+...+99+100을 계산합니까?
비재귀 솔루션:
1+2+3+...+99+100
총 99개의 추가가 수행됩니다. (반복의 개념은 여기서 소개하지 않고, 관심있는 분들은 스스로 찾아보고 배우시면 됩니다.)재귀 버전은 다음을 해결합니다.。
1과 (2+3+...+99+100)의 합을 계산합니다. (2+3+...+99+100)의 계산은 이 방법을 재사용하여 해결할 수 있습니다. , (2+3 +...+99+100)은 2를 계산하기 위해 변환되고 (3+...+99+100) 등은 두 자리 덧셈의 제한, 즉 99+를 충족합니다. 100 = 199, 그런 다음 199를 사용하여
재귀를 종료하고 결과를 계산
재귀적 가용성은 문제를 해결할 때 문제에 대한 솔루션을 직접 재사용할 수 있습니다. 이렇게 하면 실제 문제에 대한 솔루션을 크게 단순화할 수 있습니다.
이상은 아름답지만 현실은 늘 빈약하고 잔인하기까지 하다. 이더리움이 설립되었을 때 영지식 증명 도입을 고려하지 않았기 때문에 이더리움이 직접적으로 영지식 증명이라면 가장 큰 문제는 이더리움 프로토콜의 대부분의 구성 요소가 많은 수의 영지식 증명으로 이어질 것이라는 점입니다. -지식 증명 계산. 본질적으로 영지식 증명을 활용하지 않습니다. 물론 이더리움 프로토콜 자체는 시간과 기술의 발전에 따라 반복적으로 업데이트될 수 있습니다. 획기적인 합의 메커니즘이 PoW에서 PoS로 변경된 것처럼 이더리움 프로토콜의 영지식 증명은 향후 이더리움 업그레이드를 통해 달성될 수 있습니다.
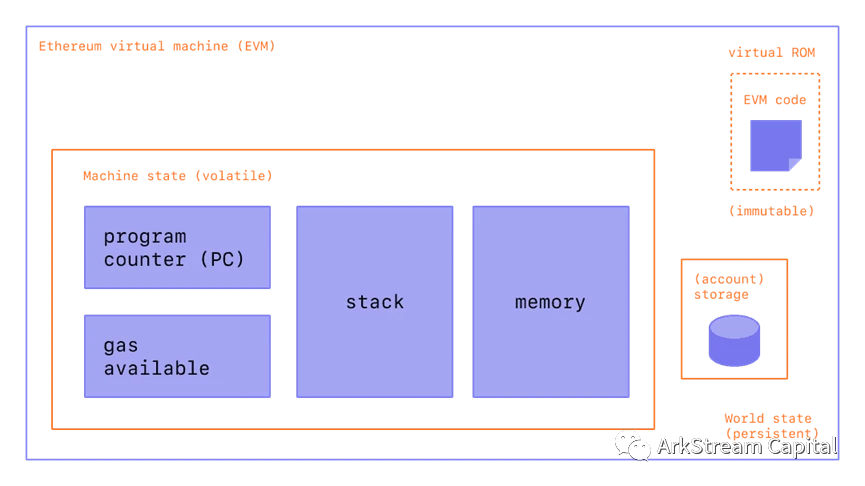
Figure 5: ETHEREUM VIRTUAL MACHINE (EVM)
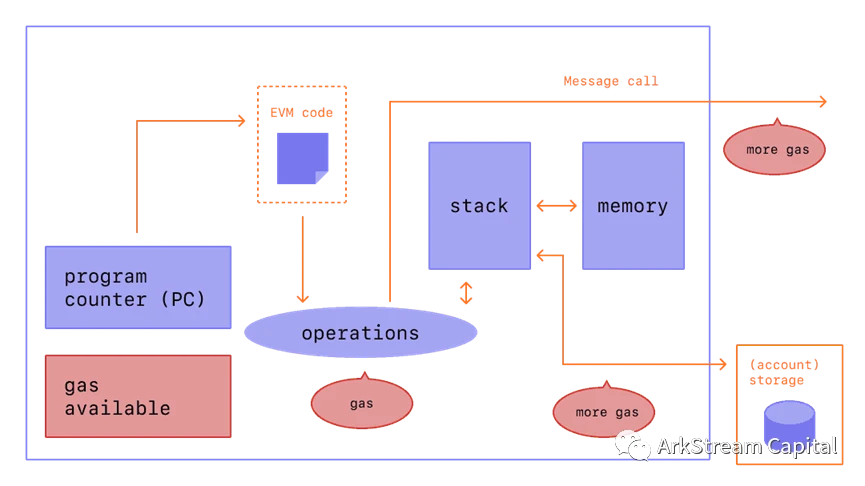
Figure 6: ETHEREUM VIRTUAL MACHINE (EVM)
이미지 설명
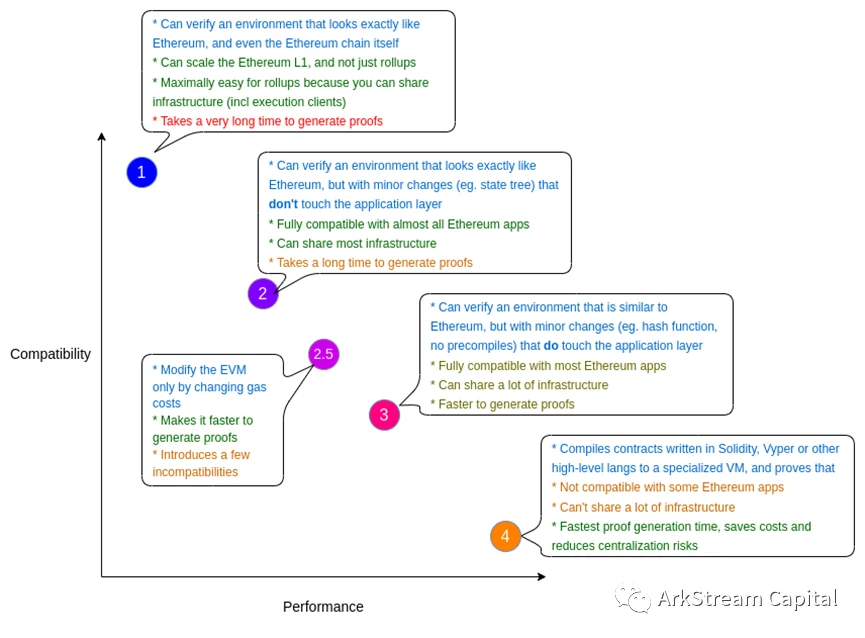
Figure 7: The different types of ZK-EVMs

Figure 8
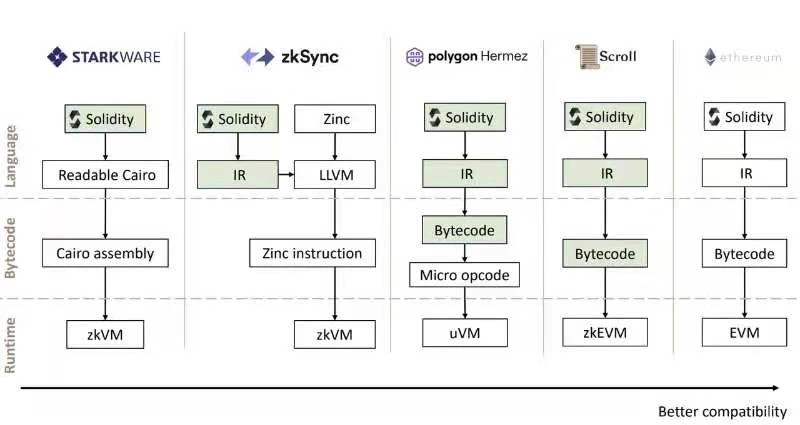
Figure 9
이미지 설명
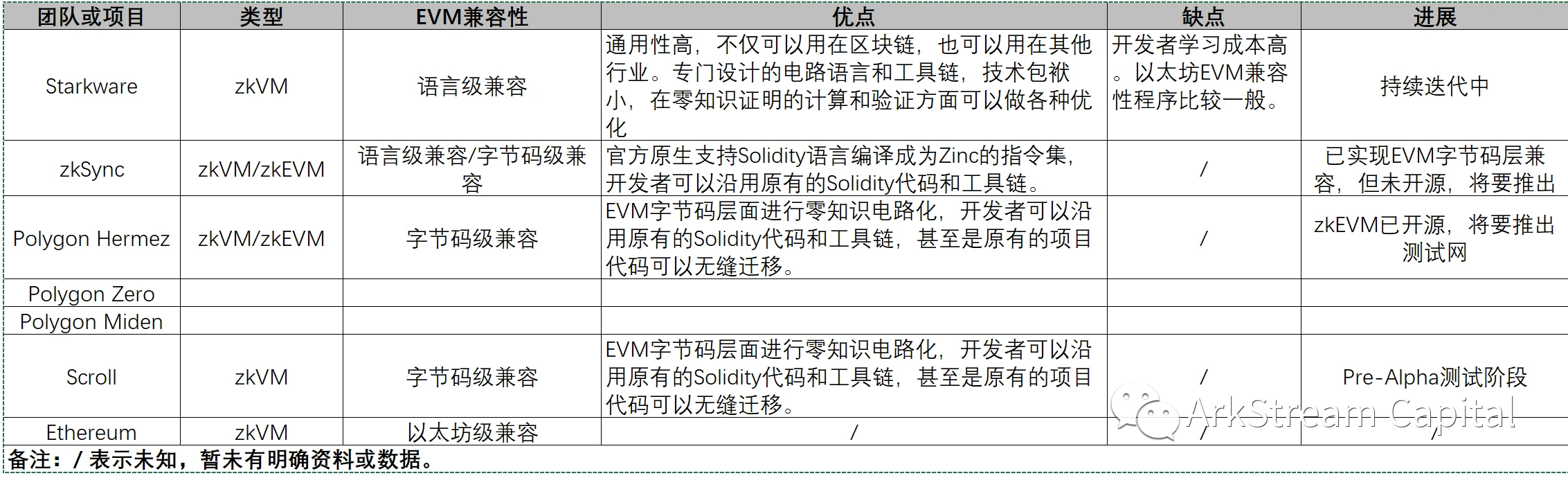
Figure 10
이미지 설명
참조:
zkVM과 zkEVM의 연구 및 구현은 서로 다른 구현 문제에 직면하고 있으며 시퀀스 종속성이 없으므로 동시에 병렬로 추진할 수 있습니다. 특정 설계 과제 및 솔루션에 대해서는 각 프로젝트의 자료 및 문서를 참조할 수 있습니다. 서로 다른 프로젝트는 zkVM/zkEVM 선택에 대한 고유한 고려 사항이 있어야 합니다.현재 대부분의 프로젝트는 zkEVM 로드에 우선 순위를 두는 경향이 있습니다.결국 이더리움 확장에 필요한 시나리오는 항상 존재했습니다. 또한 이더리움 자체의 궁극적인 ZK 목표는 완전히 호환되는 것입니다. 이렇게 생각해보면 zkEVM 연구개발을 기반으로 한 프로젝트는 향후 다양한 이더리움 라이트 노드 클라이언트로 발전할 수 있습니다. zkVM의 경우 블록체인이 파트너가 되어야 한다고 말할 수 있지만 그 먼 꿈은 블록체인에 국한되지 않습니다.
[2] https://mp.weixin.qq.com/s/808jMXvIUqB973aVHrAzGQ참조:
[1] https://github.com/sec-bit/learning-zkp/blob/master/zkp-resource-list.md 영지식 증명 학습 리소스 요약
Foresight Ventures: zk, zkVM, zkEVM의 해석 및 미래
[3] https://www.daily.news/post/5178462Scroll 연구: zkEVM 설계 과제 및 솔루션
[6] https://ethereum.org/en/developers/docs/evm/Ethereum Virtual Machine










