FHE คืออะไร
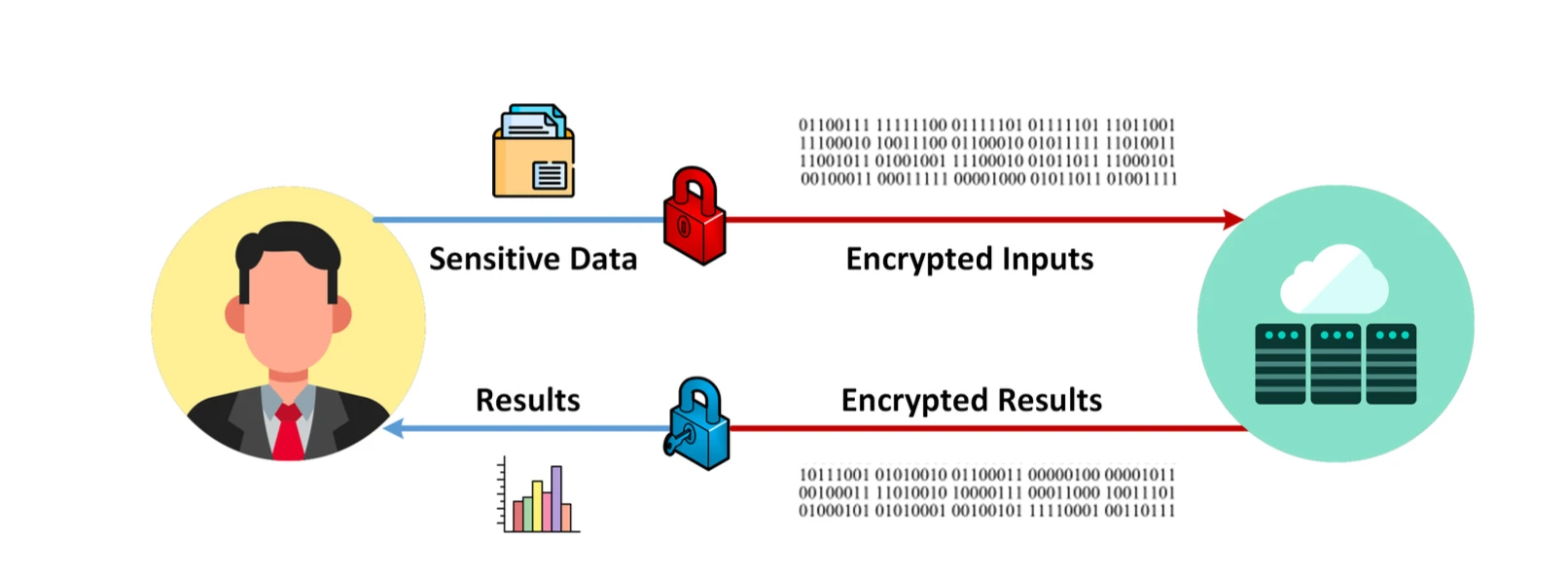
กระบวนการ FHE แหล่งที่มาของภาพ: ความเป็นส่วนตัวของข้อมูลทำได้ง่าย
FHE (การเข้ารหัสแบบโฮโมมอร์ฟิกเต็มรูปแบบ) เป็นเทคโนโลยีการเข้ารหัสขั้นสูงที่รองรับการคำนวณโดยตรงกับข้อมูลที่เข้ารหัส ซึ่งหมายความว่าข้อมูลสามารถประมวลผลได้ในขณะที่ปกป้องความเป็นส่วนตัว FHE มีสถานการณ์ที่เกี่ยวข้องมากมาย โดยเฉพาะอย่างยิ่งการประมวลผลและการวิเคราะห์ข้อมูลภายใต้การคุ้มครองความเป็นส่วนตัว เช่น การเงิน สุขภาพทางการแพทย์ การประมวลผลแบบคลาวด์ การเรียนรู้ของเครื่อง ระบบการลงคะแนน Internet of Things การคุ้มครองความเป็นส่วนตัวบล็อกเชน และสาขาอื่นๆ อย่างไรก็ตาม การค้ายังคงต้องใช้เวลาพอสมควร ปัญหาหลักคือการคำนวณและค่าใช้จ่ายด้านหน่วยความจำที่เกิดจากอัลกอริธึมนั้นมีขนาดใหญ่มากและความสามารถในการขยายขนาดไม่ดี ต่อไป เราจะอธิบายหลักการพื้นฐานของอัลกอริธึมทั้งหมดโดยย่อ และมุ่งเน้นไปที่ปัญหาที่อัลกอริธึมการเข้ารหัสนี้เผชิญ
หลักการพื้นฐาน
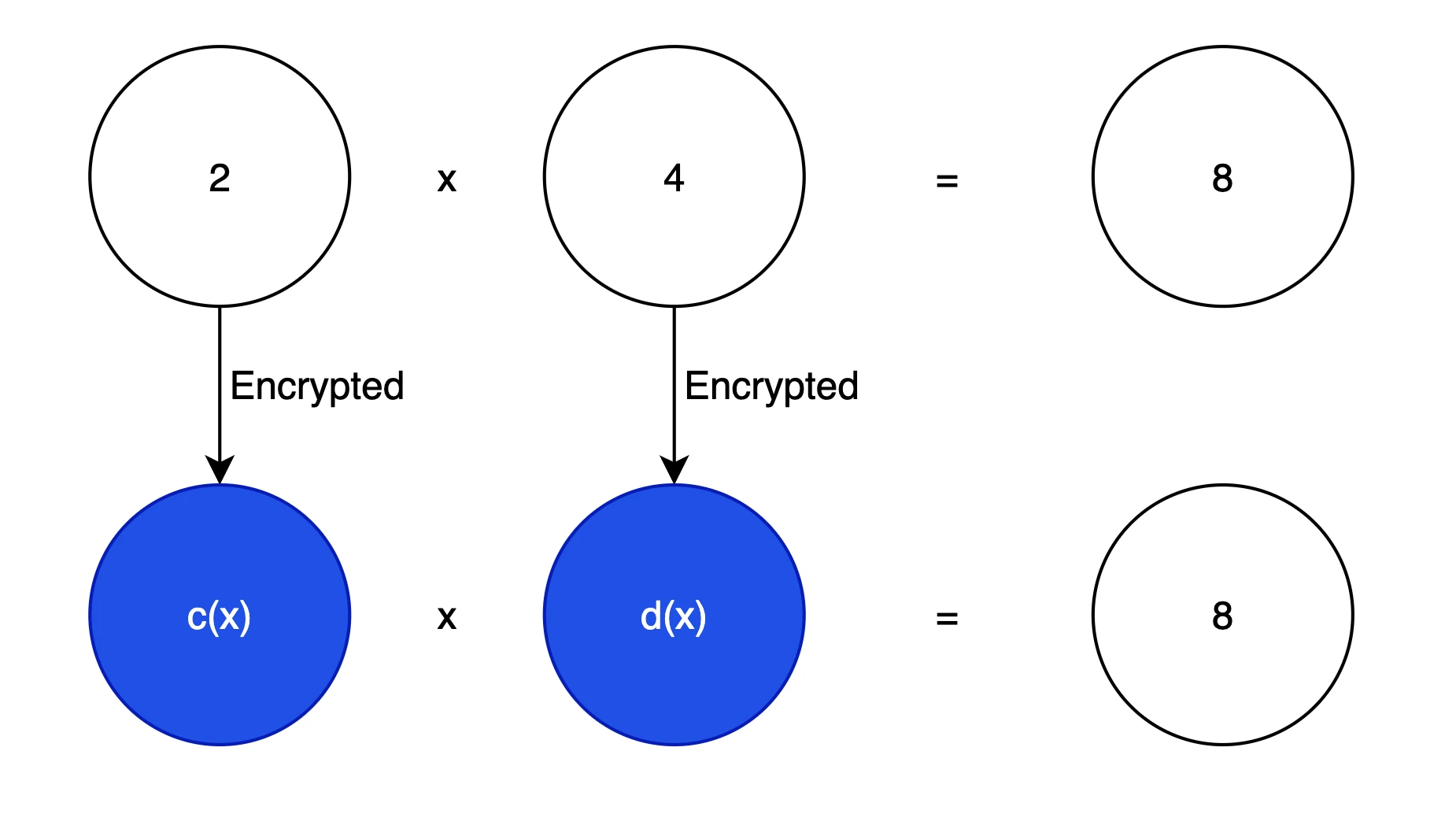
ไอคอนการเข้ารหัสโฮโมมอร์ฟิค
ขั้นแรก เราจำเป็นต้องคำนวณข้อมูลที่เข้ารหัสและยังคงได้ผลลัพธ์เดิม ซึ่งเราจะแสดงเป็นภาพดังแสดงในรูปด้านบน นี่คือเป้าหมายพื้นฐานของเรา ในวิทยาการเข้ารหัส โดยทั่วไปพหุนามมักจะใช้เพื่อซ่อนข้อมูลของข้อความต้นฉบับ เนื่องจากพหุนามสามารถแปลงเป็นปัญหาพีชคณิตเชิงเส้นได้ และยังสามารถแปลงเป็นปัญหาการคำนวณเวกเตอร์ได้ ซึ่งช่วยให้คอมพิวเตอร์สมัยใหม่ได้รับการปรับให้เหมาะสมที่สุดสำหรับเวกเตอร์ในการดำเนินการ (เช่น ในรูปแบบการคำนวณแบบขนาน) ) เช่น 3 x 2 + 2 x + 1 สามารถแสดงเป็นเวกเตอร์ [1, 2, 3]
สมมติว่าเราต้องการเข้ารหัส 2 ในระบบ HE ที่เรียบง่าย เราอาจ:
เลือกพหุนามคีย์ เช่น s(x) = 3 x 2 + 2 x + 1
สร้างพหุนามแบบสุ่ม เช่น a(x) = 2 x 2 + 5 x + 3
สร้างพหุนามที่ ผิด เล็กๆ ขึ้นมา เช่น e(x) = -1 x + 2
การเข้ารหัส 2 -> c(x) = 2 + a(x)*s(x) + e(x)
เรามาคุยกันว่าทำไมเราต้องทำเช่นนี้ สมมติว่าเราได้รับข้อความเข้ารหัส c(x) แล้ว หากเราต้องการได้ข้อความธรรมดา m สูตรคือ c(x) - e(x) - a(x) *s(x) = 2 ในที่นี้พหุนามสุ่มของเราถือว่า a(x) เป็นแบบสาธารณะ ดังนั้นเราเพียงแต่ต้องแน่ใจว่าคีย์ s(x) ของเราเป็นความลับ หากเรารู้ s(x) บวก c(x) หากข้อผิดพลาดมีขนาดเล็กมาก ในทางทฤษฎีก็สามารถละเว้นได้ และสามารถรับข้อความธรรมดา m ได้
นี่คือคำถามแรก มีพหุนามมากมาย จะเลือกพหุนามได้อย่างไร? พหุนามระดับที่ดีที่สุดคืออะไร? อันที่จริงแล้ว ระดับของพหุนามนั้นถูกกำหนดโดยอัลกอริธึมที่ใช้ในการนำ HE ไปใช้ โดยปกติแล้วจะมีกำลัง 2 เช่น 1024/2048 เป็นต้น ค่าสัมประสิทธิ์ของพหุนามจะถูกสุ่มเลือกจากสนามจำกัด q เช่น mod 10000 จากนั้นเลือกแบบสุ่มจาก 0-9999 มีอัลกอริธึมมากมายสำหรับการเลือกสัมประสิทธิ์แบบสุ่ม เช่น การแจกแจงแบบสม่ำเสมอ การแจกแจงแบบเกาส์เซียนแบบไม่ต่อเนื่อง เป็นต้น รูปแบบที่แตกต่างกันยังมีข้อกำหนดในการเลือกค่าสัมประสิทธิ์ที่แตกต่างกัน โดยปกติเพื่อให้เป็นไปตามหลักการแก้ปัญหาอย่างรวดเร็วภายใต้โครงการ
คำถามที่สอง เสียงคืออะไร? สัญญาณรบกวนถูกใช้เพื่อสร้างความสับสนให้กับผู้โจมตี เนื่องจากสมมติว่าตัวเลขทั้งหมดของเราคือ s(x) และพหุนามสุ่มอยู่ในโดเมน ก็จะมีกฎบางอย่างอยู่ ตราบใดที่ข้อความธรรมดา m ถูกป้อนเข้ามาหลายครั้งตามผลลัพธ์ c(x) คุณสามารถตัดสินข้อมูลของทั้งสอง s(x) และ c(x) ได้ หากมีการใช้สัญญาณรบกวน e(x) รับประกันได้ว่า s(x) และ c(x) ไม่สามารถรับได้จากการแจงนับง่ายๆ ซ้ำๆ เนื่องจากมีข้อผิดพลาดเล็กๆ น้อยๆ แบบสุ่มโดยสมบูรณ์ พารามิเตอร์นี้เรียกอีกอย่างว่า Noise Budget สมมติว่า q = 2^32 เสียงเริ่มต้นอาจอยู่ที่ประมาณ 2^3 หลังจากการดำเนินการบางอย่าง เสียงรบกวนอาจเพิ่มขึ้นเป็น 2^20 ณ จุดนี้ยังมีพื้นที่เพียงพอสำหรับการถอดรหัส เนื่องจาก 2^20 << 2^32
หลังจากที่เราได้รับพหุนามแล้ว ตอนนี้เราจำเป็นต้องแปลงการดำเนินการ c(x) * d(x) เป็น วงจร ซึ่งมักจะปรากฏใน ZKP เนื่องจากแนวคิดเชิงนามธรรมของวงจรจัดให้มีแบบจำลองการคำนวณทั่วไปเพื่อเป็นตัวแทนใดๆ การคำนวณและแบบจำลองวงจรช่วยให้ติดตามและจัดการสัญญาณรบกวนที่เกิดขึ้นจากการดำเนินการแต่ละครั้งได้อย่างแม่นยำ และยังอำนวยความสะดวกในการแนะนำฮาร์ดแวร์ระดับมืออาชีพในภายหลัง เช่น ASIC และ FPGA เพื่อการคำนวณแบบเร่ง เช่น โมเดล SIMD การดำเนินการที่ซับซ้อนใดๆ สามารถแมปเข้ากับองค์ประกอบวงจรโมดูลาร์อย่างง่าย เช่น การบวกและการคูณ

การแสดงวงจรเลขคณิต
การบวกและการคูณสามารถแสดงการลบและการหาร รวมถึงการคำนวณใดๆ ก็ได้ ค่าสัมประสิทธิ์ของพหุนามจะแสดงในรูปแบบไบนารีและเรียกว่าอินพุตของวงจร แต่ละโหนดวงจรแสดงถึงการบวกหรือการคูณที่ดำเนินการ แต่ละ (*) แทนประตูการคูณ และแต่ละ (+) แทนประตูบวก นี่คือวงจรอัลกอริทึม
สิ่งนี้ทำให้เกิดคำถาม เพื่อไม่ให้ข้อมูลเชิงความหมายรั่วไหล เราขอแนะนำ e(x) ซึ่งเรียกว่าสัญญาณรบกวน ในการคำนวณของเรา การบวกจะเปลี่ยนพหุนาม e(x) สองตัวเป็นพหุนามที่มีดีกรีเท่ากัน ในการคูณ การคูณของพหุนามเสียงสองตัวจะเพิ่มระดับของ e(x) และขนาดของข้อความแบบทวีคูณ หากเสียงมีขนาดใหญ่เกินไป ไม่สามารถละเลยสัญญาณรบกวนได้ในระหว่างการคำนวณผลลัพธ์ และข้อความต้นฉบับ m ไม่สามารถกู้คืนได้ นี่เป็นเหตุผลสำคัญที่จำกัดความสามารถของอัลกอริธึม HE ในการแสดงการคำนวณตามอำเภอใจ เนื่องจากสัญญาณรบกวนเพิ่มขึ้นแบบทวีคูณ และถึงเกณฑ์ที่ใช้ไม่ได้อย่างรวดเร็ว ในวงจร สิ่งนี้เรียกว่าความลึกของวงจร และจำนวนการดำเนินการคูณคือค่าความลึกของวงจร
หลักการพื้นฐานของการเข้ารหัสโฮโมมอร์ฟิก HE แสดงอยู่ในภาพด้านบน เพื่อแก้ไขปัญหาสัญญาณรบกวนที่จำกัดการเข้ารหัสโฮโมมอร์ฟิก จึงได้มีการเสนอวิธีแก้ปัญหาจำนวนหนึ่ง:
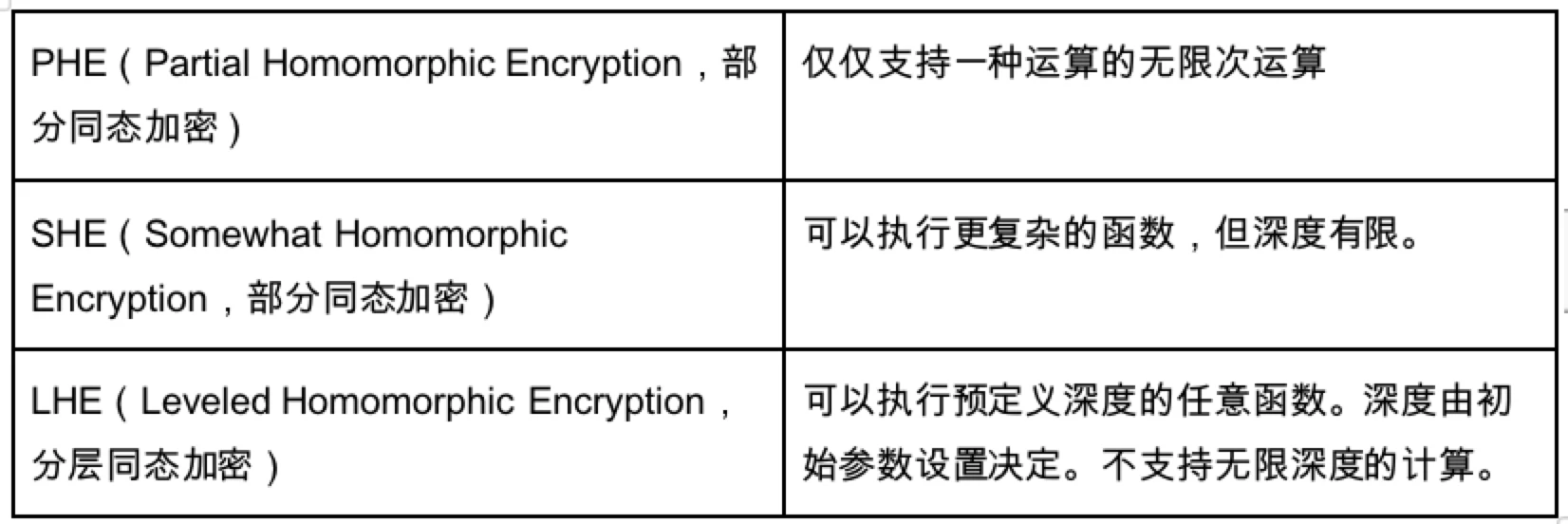
LHE เป็นอัลกอริทึมที่เหมาะสมมากที่นี่ เพราะภายใต้อัลกอริทึมนี้ ตราบใดที่กำหนดความลึก ฟังก์ชันใดๆ ก็สามารถดำเนินการภายในความลึกได้ แต่ PHE และ SHE ไม่สามารถบรรลุความสมบูรณ์ของทัวริงได้ ดังนั้น บนพื้นฐานนี้ นักเข้ารหัสจึงทำการวิจัยและเสนอเทคโนโลยี 3 รายการเพื่อสร้างการเข้ารหัส FHE แบบโฮโมมอร์ฟิกโดยสมบูรณ์ โดยหวังว่าจะตระหนักถึงวิสัยทัศน์ของการดำเนินฟังก์ชันตามอำเภอใจในระดับความลึกที่ไม่สิ้นสุด
การสลับคีย์: หลังจากที่เราคูณ ขนาดของไซเฟอร์เท็กซ์จะเพิ่มขึ้นแบบทวีคูณ ซึ่งจะทำให้มีความต้องการหน่วยความจำและทรัพยากรการประมวลผลอย่างมากสำหรับการดำเนินการในภายหลัง ดังนั้น การใช้การสลับคีย์หลังจากการคูณแต่ละครั้งสามารถบีบอัดได้ แต่จะทำให้เกิดเสียงรบกวนเล็กน้อย .
การสลับโมดูลัส: ไม่ว่าจะเป็นการคูณหรือการสลับคีย์ สัญญาณรบกวนจะเพิ่มขึ้นแบบเอกซ์โปเนนเชียล q คือ Mod 10000 ที่เราพูดถึงก่อนหน้านี้ พารามิเตอร์สามารถรับได้ใน [0, 9999] เท่านั้น หลังจากการคำนวณหลายครั้ง สัญญาณรบกวนสุดท้ายยังคงอยู่ภายใน q และสามารถถอดรหัสได้ ดังนั้น หลังจากการดำเนินการหลายครั้ง เพื่อป้องกันไม่ให้ดัชนีเสียงรบกวนเพิ่มขึ้นเกินเกณฑ์ จำเป็นต้องใช้ Modulus Switching เพื่อลดงบประมาณด้านเสียง เพื่อให้สามารถระงับเสียงรบกวนได้ เราสามารถหาหลักการพื้นฐานได้ที่นี่ หากการคำนวณของเราซับซ้อนและความลึกของวงจรมีขนาดใหญ่ ก็จำเป็นต้องใช้โมดูลัส q สัญญาณรบกวนที่มากขึ้นเพื่อรองรับความพร้อมใช้งานหลังจากเพิ่มขึ้นแบบเอ็กซ์โพเนนเชียลหลายครั้ง
Bootstrap: แต่ถ้าคุณต้องการบรรลุการคำนวณเชิงลึกที่ไม่มีที่สิ้นสุด Modulus สามารถจำกัดการเติบโตของสัญญาณรบกวนเท่านั้น แต่สวิตช์แต่ละตัวจะทำให้ช่วง q เล็กลง เรารู้ว่าเมื่อลดลงแล้ว จะต้องมีความซับซ้อนในการคำนวณมากขึ้น ลดลง Bootstrap เป็นเทคโนโลยีใหม่ที่จะรีเซ็ตเสียงรบกวนให้อยู่ในระดับเดิม แทนที่จะลดเสียงรบกวน Bootstrap ไม่จำเป็นต้องลดโมดูลัส จึงสามารถรักษาพลังการประมวลผลของระบบได้ แต่ข้อเสียคือต้องใช้ทรัพยากรคอมพิวเตอร์จำนวนมาก
โดยทั่วไป สำหรับการคำนวณภายใต้ขั้นตอนที่จำกัด การใช้ Modulus Switching สามารถลดสัญญาณรบกวนได้ แต่จะยังลดโมดูลัสซึ่งก็คืองบประมาณของสัญญาณรบกวนด้วย ส่งผลให้ความสามารถในการคำนวณถูกบีบอัด นี่เป็นเพียงการคำนวณในขั้นตอนที่จำกัดเท่านั้น Bootstrap สามารถใช้การรีเซ็ตสัญญาณรบกวนได้ ดังนั้นตามอัลกอริธึม LHE จึงสามารถบรรลุ FHE ที่แท้จริง ซึ่งก็คือการคำนวณฟังก์ชันใดๆ ที่ไม่มีที่สิ้นสุด และนี่ก็เป็นความหมายของ FHE เต็มรูปแบบด้วย
อย่างไรก็ตาม ข้อเสียก็เห็นได้ชัดเช่นกันว่าต้องใช้ทรัพยากรคอมพิวเตอร์จำนวนมาก ดังนั้น ภายใต้สถานการณ์ปกติ จึงมีการใช้เทคโนโลยีลดเสียงรบกวนทั้งสองนี้ร่วมกัน บูตสแตรปที่มีราคาแพงกว่าในการคำนวณจะถูกใช้เมื่อการเปลี่ยนโมดูลัสไม่สามารถควบคุมเสียงรบกวนได้อย่างมีประสิทธิภาพอีกต่อไป
โซลูชัน FHE ในปัจจุบันมีการใช้งานเฉพาะต่อไปนี้ ซึ่งทั้งหมดใช้เทคโนโลยีหลักของ Bootstrap:
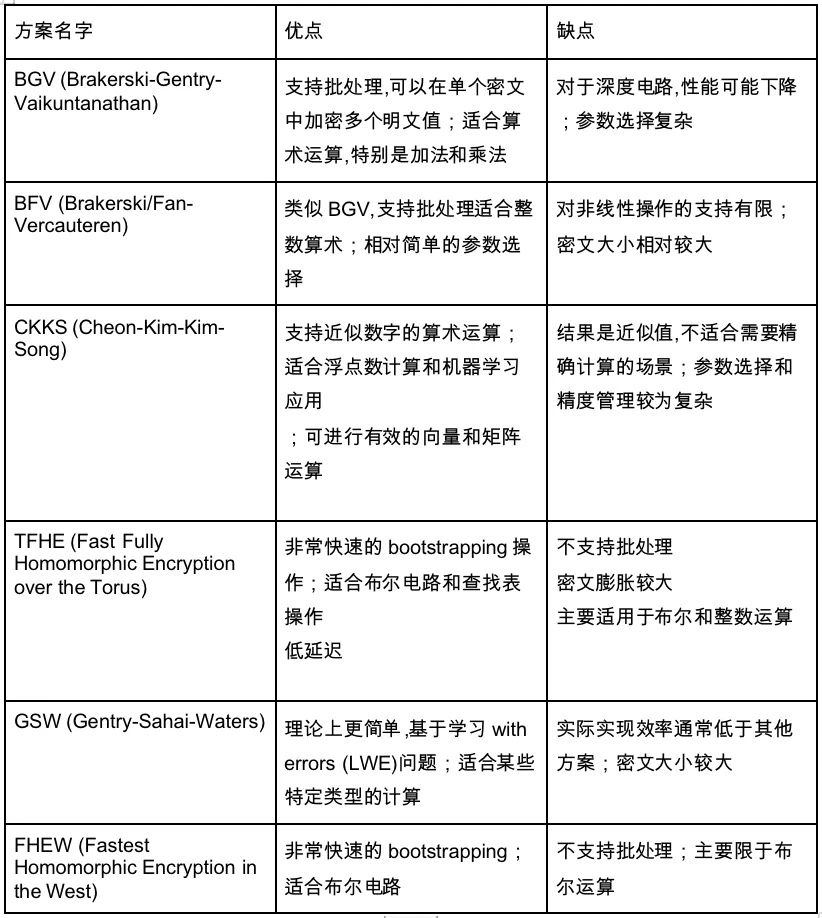
สิ่งนี้ยังนำไปสู่ประเภทของวงจรที่เราไม่ได้พูดถึง วงจรหลักที่เราแนะนำข้างต้นคือวงจรทางคณิตศาสตร์ แต่มีวงจรอีกประเภทหนึ่ง - วงจรบูลีน วงจรเลขคณิตค่อนข้างเป็นนามธรรม เช่น 1+1 โหนดยังเป็นการบวกหรือการหาร ในขณะที่ตัวเลขทั้งหมดในวงจรบูลีนจะถูกแปลงเป็นฐาน 01 และโหนดทั้งหมดเป็นการดำเนินการบูล รวมถึงการดำเนินการ NOT, OR และ AND คล้ายกับการใช้วงจรคอมพิวเตอร์ของเรา วงจรเลขคณิตเป็นวงจรนามธรรม
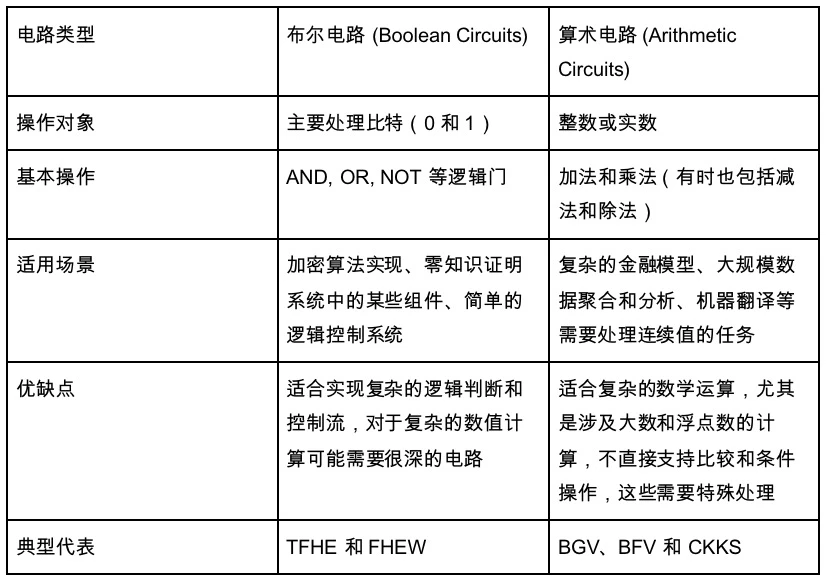
ดังนั้น เราจึงมองคร่าวๆ ได้ว่าการดำเนินการแบบบูลีนเป็นการประมวลผลที่ยืดหยุ่นซึ่งใช้ข้อมูลมากน้อยกว่า ในขณะที่การดำเนินการทางคณิตศาสตร์เป็นโซลูชันสำหรับแอปพลิเคชันที่ใช้ข้อมูลจำนวนมาก
ปัญหาที่ FHE เผชิญ
เนื่องจากการคำนวณของเราจำเป็นต้องได้รับการเข้ารหัสแล้วแปลงเป็น วงจร และเนื่องจากการคำนวณอย่างง่ายจะคำนวณเพียง 2+4 เท่านั้น แต่หลังจากการเข้ารหัส จึงมีการใช้กระบวนการคำนวณทางอ้อมที่เข้ารหัสลับจำนวนมาก รวมถึงเทคโนโลยีล้ำสมัยบางอย่าง เช่น เป็น Bootstrap เพื่อแก้ปัญหาเสียงรบกวน ซึ่งส่งผลให้ต้นทุนการคำนวณมีขนาด N สูงกว่าการคำนวณทั่วไป
เราใช้ตัวอย่างจากโลกแห่งความเป็นจริงเพื่อให้ผู้อ่านรู้สึกถึงความโอเวอร์เฮดของกระบวนการเข้ารหัสเพิ่มเติมเหล่านี้ในทรัพยากรการประมวลผล สมมติว่าการคำนวณปกติใช้เวลาประมาณ 200 รอบสัญญาณนาฬิกาบนโปรเซสเซอร์ 3 GHz การถอดรหัส AES-128 ปกติจะใช้เวลาประมาณ 67 นาโนวินาที (200/3 GHz) รุ่น FHE ใช้เวลา 35 วินาที ซึ่งนานกว่ารุ่นปกติประมาณ 522,388,060 เท่า (35/67 e-9) นั่นคือ การใช้ทรัพยากรคอมพิวเตอร์เดียวกัน อัลกอริธึมธรรมดาเดียวกัน และอัลกอริธึมภายใต้การคำนวณ FHE ความต้องการทรัพยากรคอมพิวเตอร์จะอยู่ที่ประมาณ 500 ล้านครั้ง

โปรแกรม DARPA dprive ที่มา: DARPA
เพื่อประโยชน์ของความปลอดภัยของข้อมูล DARPA ในสหรัฐอเมริกาได้สร้างโปรแกรม Dprive ขึ้นมาเป็นพิเศษในปี 2021 โดยเชิญทีมวิจัยหลายทีม รวมถึง Microsoft, Intel และอื่นๆ เป้าหมายของพวกเขาคือการสร้างตัวเร่งความเร็ว FHE และรองรับชุดซอฟต์แวร์เพื่อสร้างความเร็วในการประมวลผล FHE สอดคล้องกับการดำเนินการที่คล้ายกันกับข้อมูลที่ไม่ได้เข้ารหัสมากขึ้น บรรลุเป้าหมายของความเร็วในการคำนวณ FHE ที่ประมาณ 1/10 ของการคำนวณทั่วไป Tom Rondeau ผู้จัดการโปรแกรม DARPA กล่าวว่า มีการประเมินว่าในโลก FHE การคำนวณของเราช้ากว่าในโลกข้อความธรรมดาประมาณล้านเท่า
Dprive มุ่งเน้นไปที่ประเด็นต่อไปนี้เป็นหลัก:
เพิ่มความยาวคำของโปรเซสเซอร์: ระบบคอมพิวเตอร์สมัยใหม่ใช้ความยาวคำ 64 บิต กล่าวคือ ตัวเลขสามารถมีได้สูงสุด 64 บิต แต่จริงๆ แล้ว q มักจะเท่ากับ 1,024 บิต หากเราต้องการบรรลุเป้าหมายนี้ เราต้องแยก q ของเรา ซึ่งจะส่งผลต่อทรัพยากรหน่วยความจำและการสูญเสียความเร็ว ดังนั้น เพื่อให้บรรลุ q ที่ใหญ่ขึ้น เราจำเป็นต้องสร้างโปรเซสเซอร์ที่มีขนาดคำ 1,024 บิตหรือใหญ่กว่า ฟิลด์ที่มีขอบเขตจำกัด q มีความสำคัญมาก ดังที่เราได้กล่าวไปแล้ว ยิ่งมีขนาดใหญ่เท่าใดก็ยิ่งสามารถคำนวณขั้นตอนได้มากขึ้นเท่านั้น q มีบทบาทสำคัญใน FHE ซึ่งส่งผลกระทบต่อเกือบทุกแง่มุมของโครงการ รวมถึงความปลอดภัย ประสิทธิภาพ จำนวนการคำนวณที่สามารถทำได้ และทรัพยากรหน่วยความจำที่ต้องการ
การสร้างโปรเซสเซอร์ ASIC: ดังที่เราได้กล่าวไปแล้ว เพื่อความสะดวกในการขนานและเหตุผลอื่นๆ เราได้สร้างพหุนามและสร้างวงจรผ่านพหุนาม ซึ่งคล้ายกับ ZK CPU และ GPU ปัจจุบันไม่มีความสามารถนี้ (ทรัพยากรคอมพิวเตอร์และทรัพยากรหน่วยความจำ) ในการรันวงจร และจำเป็นต้องสร้างโปรเซสเซอร์ ASIC เฉพาะทางเพื่อรองรับอัลกอริทึม FHE
สร้างสถาปัตยกรรมแบบขนาน MIMD ต่างจากสถาปัตยกรรมแบบขนาน SIMD ตรงที่ SIMD สามารถดำเนินการคำสั่งเดียวกับข้อมูลหลายรายการเท่านั้น ซึ่งก็คือ การแยกข้อมูลและการประมวลผลแบบขนาน แต่ MIMD สามารถแยกข้อมูลและใช้คำสั่งที่แตกต่างกันในการคำนวณได้ SIMD ส่วนใหญ่จะใช้สำหรับข้อมูลแบบขนาน ซึ่งเป็นสถาปัตยกรรมหลักสำหรับการประมวลผลธุรกรรมแบบขนานในโครงการบล็อกเชนส่วนใหญ่ MIMD สามารถจัดการงานแบบขนานได้หลายประเภท MIMD มีความซับซ้อนในทางเทคนิคมากกว่า และต้องมุ่งเน้นไปที่ปัญหาการซิงโครไนซ์และการสื่อสาร
เหลือเวลาเพียงหนึ่งเดือนก่อนที่โปรแกรม DEPRIVE ของ DARPA จะหมดอายุ แผนเดิมสำหรับ Dprvie จะเริ่มในปี 2021 และสิ้นสุดแผนสามเฟสในเดือนกันยายน 2024 อย่างไรก็ตาม ดูเหมือนว่าความคืบหน้าจะช้าและยังไม่บรรลุตามที่คาดไว้ ระดับประสิทธิภาพเป้าหมาย 1/10 เมื่อเทียบกับการคำนวณทั่วไป
แม้ว่าความคืบหน้าในการเจาะผ่านเทคโนโลยี FHE จะช้า แต่ก็คล้ายกับเทคโนโลยี ZK แต่ก็ประสบปัญหาร้ายแรงที่การใช้งานฮาร์ดแวร์เป็นข้อกำหนดเบื้องต้นสำหรับการใช้เทคโนโลยี อย่างไรก็ตาม เรายังคงเชื่อว่าในระยะยาว เทคโนโลยี FHE ยังคงมีความสำคัญเฉพาะตัว โดยเฉพาะอย่างยิ่งในการปกป้องความเป็นส่วนตัวของข้อมูลที่ปลอดภัยบางส่วนที่ระบุไว้ในส่วนแรก สำหรับ DARPA กระทรวงกลาโหมมีข้อมูลที่ละเอียดอ่อนจำนวนมาก หากต้องการเผยแพร่ความสามารถทั่วไปของ AI ให้กับกองทัพ ก็ต้องฝึกอบรม AI ในรูปแบบของความปลอดภัยของข้อมูล ไม่เพียงเท่านั้น ยังใช้ได้กับข้อมูลที่ละเอียดอ่อนที่สำคัญ เช่น การแพทย์และการเงิน จริงๆ แล้ว FHE ไม่เหมาะสำหรับการคำนวณทั่วไปทั้งหมด แต่จะเน้นไปที่ความต้องการด้านการประมวลผลของข้อมูลที่ละเอียดอ่อนมากกว่า ยุคหลังควอนตัม
สำหรับเทคโนโลยีที่ล้ำสมัยนี้ จะต้องพิจารณาถึงความแตกต่างของเวลาระหว่างวงจรการลงทุนและการดำเนินการเชิงพาณิชย์ ดังนั้นเราจึงต้องระมัดระวังอย่างมากเกี่ยวกับระยะเวลาการดำเนินการของ FHE
การรวมกันของบล็อคเชน
ในบล็อกเชนนั้น FHE ยังใช้เพื่อปกป้องความเป็นส่วนตัวของข้อมูลเป็นหลัก พื้นที่การใช้งาน ได้แก่ ความเป็นส่วนตัวแบบออนไลน์ ความเป็นส่วนตัวของข้อมูลการฝึกอบรม AI ความเป็นส่วนตัวในการลงคะแนนแบบออนไลน์ การตรวจสอบธุรกรรมความเป็นส่วนตัวแบบออนไลน์ ฯลฯ หนึ่งในนั้นคือ FHE ยังเป็นที่รู้จักว่าเป็นหนึ่งในโซลูชันที่มีศักยภาพสำหรับโซลูชัน MEV แบบออนไลน์ ตามบทความ MEV ของเรา การส่องสว่างป่ามืด - การเปิดเผยความลึกลับของ MEV โซลูชัน MEV ในปัจจุบันจำนวนมากเป็นเพียงวิธีในการสร้างสถาปัตยกรรม MEV ขึ้นมาใหม่ ไม่ใช่วิธีแก้ปัญหา จริงๆ แล้วการโจมตีแบบแซนวิชทำให้เกิดปัญหา UX ยังไม่ได้รับการแก้ไข วิธีแก้ปัญหาที่เราคิดในตอนแรกคือการเข้ารหัสธุรกรรมโดยตรงโดยยังคงรักษาสถานะไว้เป็นสาธารณะ
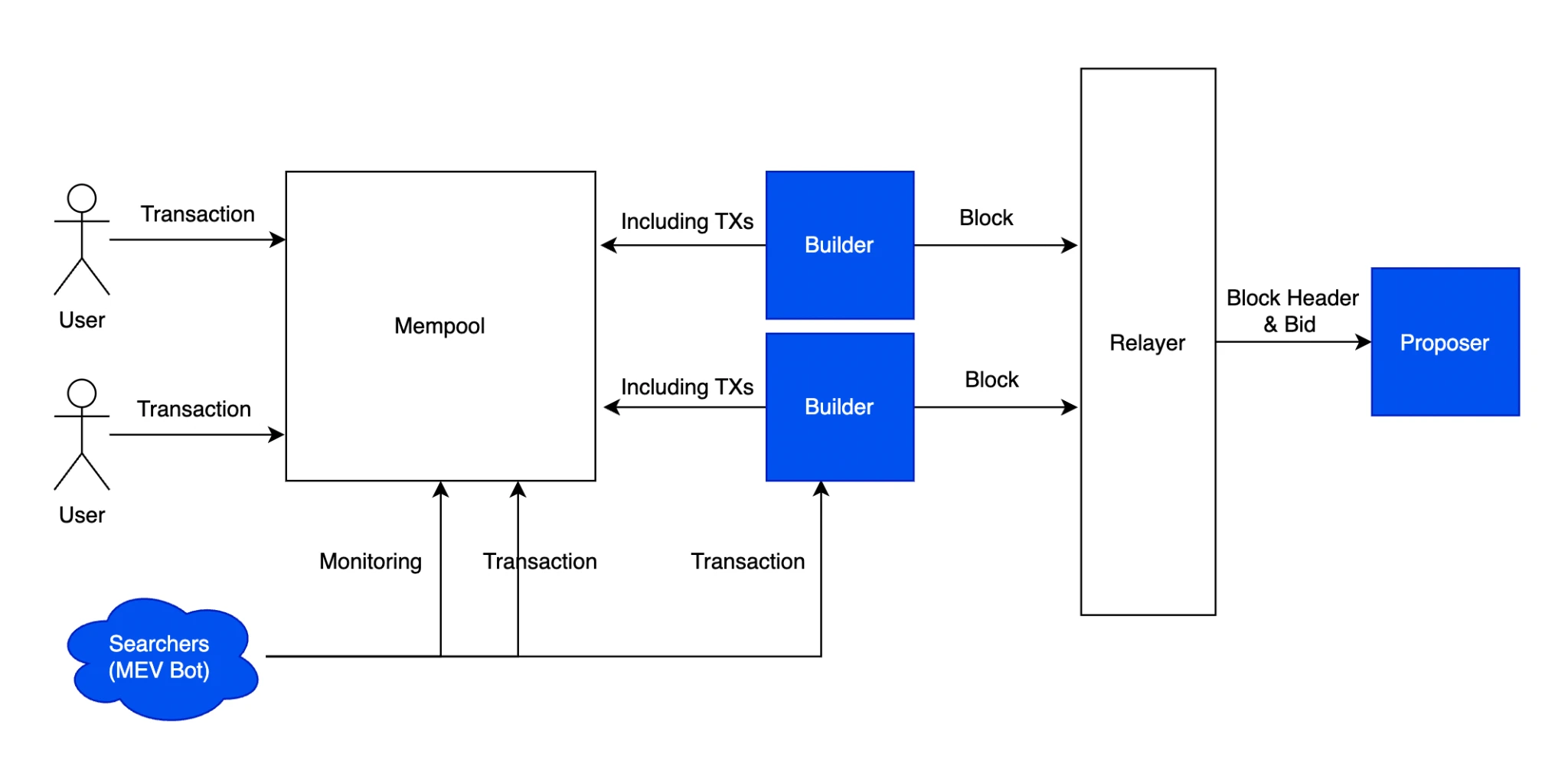
กระบวนการ MEV PBS
แต่ยังมีปัญหาอยู่เช่นกันว่าหากเราเข้ารหัสธุรกรรมอย่างสมบูรณ์ ผลกระทบภายนอกเชิงบวกที่บอท MEV นำมาจะหายไปในเวลาเดียวกัน เพื่อตรวจสอบความถูกต้องของธุรกรรม การพิจารณาความถูกต้องของสถานะสุดท้ายจะเพิ่มข้อกำหนดในการรันโหนดอย่างมีนัยสำคัญ ส่งผลให้ปริมาณงานของเครือข่ายทั้งหมดช้าลงหนึ่งล้านเท่า
โครงการหลัก
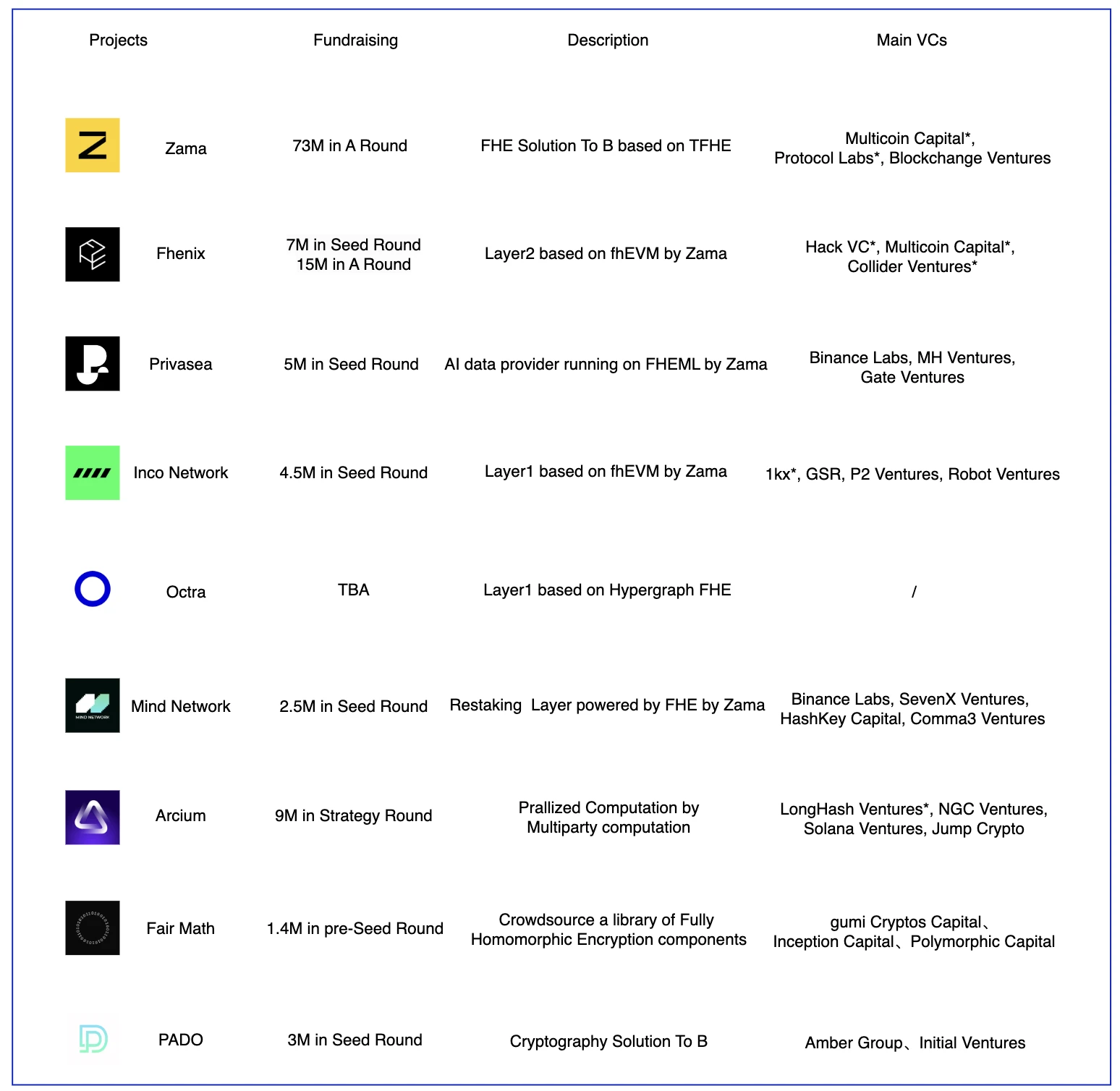
FHE ภูมิทัศน์
FHE เป็นเทคโนโลยีที่ค่อนข้างใหม่ เทคโนโลยี FHE ส่วนใหญ่ที่ใช้ในปัจจุบันโดยโครงการต่างๆ สร้างขึ้นโดย Zama เช่น Fhenix, Privasea, Inco Network และ Mind Network ความสามารถในการใช้งานด้านวิศวกรรม FHE ของ Zama ได้รับการยอมรับในโครงการเหล่านี้ โครงการข้างต้นส่วนใหญ่สร้างขึ้นจากห้องสมุดที่ Zama จัดหาให้ ความแตกต่างที่สำคัญอยู่ที่รูปแบบธุรกิจ Fhenix หวังที่จะสร้าง Optimism Layer 2 ที่ให้ความสำคัญกับความเป็นส่วนตัวเป็นอันดับแรก และ Privasea หวังว่าจะใช้ความสามารถของ FHE เพื่อดำเนินการกับข้อมูล LLM อย่างไรก็ตาม นี่เป็นการดำเนินการที่ต้องใช้ข้อมูลจำนวนมาก ซึ่งต้องใช้ข้อกำหนดด้านเทคนิคและฮาร์ดแวร์ที่สูงมากสำหรับ FHE ตาม TFHE อาจไม่ใช่ตัวเลือกที่ดีที่สุด ทั้ง Inco Network และ Fhenix ใช้ fhEVM แต่อันหนึ่งสร้างขึ้นบนเลเยอร์ 1 และอีกอันบนเลเยอร์ 2 Arcium สร้างขึ้นจากการผสมผสานเทคโนโลยีการเข้ารหัสที่หลากหลาย รวมถึง FHE, MPC และ ZK โมเดลธุรกิจของ Mind Network ค่อนข้างแตกต่าง โดยเลือกแนวทาง Reslogging เพื่อแก้ไขปัญหาความมั่นคงทางเศรษฐกิจและความไว้วางใจในการลงคะแนนเสียงในระดับฉันทามติ โดยจัดให้มีการรักษาสภาพคล่องและสถาปัตยกรรมซับเน็ตที่ใช้ FHE
ซามา
Zama เป็นโซลูชันที่ใช้ TFHE ซึ่งโดดเด่นด้วยการใช้เทคโนโลยี Bootstrap ซึ่งมุ่งเน้นไปที่การประมวลผลการดำเนินการแบบบูลีนและการดำเนินการจำนวนเต็มคำที่มีความยาวต่ำ แม้ว่าจะเป็นการใช้งานทางเทคนิคที่เร็วกว่าในโซลูชัน FHE ของเรา แต่ก็ยังสามารถเปรียบเทียบกับ There ได้ ช่องว่างที่ใหญ่มากกับการคำนวณแบบธรรมดา ประการที่สอง เป็นไปไม่ได้เลยที่จะดำเนินการคำนวณโดยพลการ เมื่อเผชิญกับงานที่ต้องใช้ข้อมูลมาก การดำเนินการเหล่านี้จะทำให้ความลึกของวงจรใหญ่เกินกว่าจะประมวลผลได้ ไม่ใช่โซลูชันที่เน้นข้อมูลและใช้ได้กับขั้นตอนสำคัญบางขั้นตอนของกระบวนการเข้ารหัสเท่านั้น
ปัจจุบัน TFHE มีโค้ดการใช้งานสำเร็จรูป งานหลักของ Zama คือการเขียน TFHE ใหม่โดยใช้ภาษา Rust ซึ่งเป็นลัง rs-TFHE ในเวลาเดียวกัน เพื่อที่จะลดเกณฑ์สำหรับผู้ใช้ Rust ลง ยังได้สร้างเครื่องมือการคอมไพล์ Concrate ซึ่งสามารถแปลง Python ให้เทียบเท่ากับ rs-TFHE เมื่อใช้เครื่องมือนี้ คุณสามารถแปลภาษาโมเดลขนาดใหญ่ที่ใช้ Python เป็นภาษาสนิมตาม TFHE-rs ได้ ด้วยวิธีนี้ โมเดลขนาดใหญ่ที่ใช้การเข้ารหัสโฮโมมอร์ฟิกจึงสามารถรันได้ แต่งานที่ต้องใช้ข้อมูลมากในขณะนี้ไม่เหมาะกับสถานการณ์ TFHE ผลิตภัณฑ์ fhEVM ของ Zama เป็นเทคโนโลยีที่ใช้การเข้ารหัสโฮโมมอร์ฟิก (FHE) เต็มรูปแบบเพื่อใช้สัญญาอัจฉริยะที่เป็นความลับบน EVM และสามารถรองรับสัญญาอัจฉริยะที่เข้ารหัสจากต้นทางถึงปลายทางที่คอมไพล์ตามภาษา Solidity
โดยทั่วไป ในฐานะผลิตภัณฑ์ To B Zama ได้สร้างสแต็กการพัฒนา blockchain + AI ที่ค่อนข้างสมบูรณ์โดยอิงจาก TFHE สามารถช่วยโครงการ web3 สร้างโครงสร้างพื้นฐานและแอปพลิเคชัน FHE ได้อย่างง่ายดาย
ออคตร้า
สิ่งที่พิเศษเกี่ยวกับ Octra คือการใช้เทคโนโลยีที่แตกต่างในการใช้งาน FHE ใช้เทคโนโลยีที่เรียกว่าไฮเปอร์กราฟเพื่อใช้บูตสแตรป นอกจากนี้ยังใช้วงจรบูลีนด้วย แต่ Octra เชื่อว่าเทคโนโลยีที่ใช้ไฮเปอร์กราฟสามารถบรรลุ FHE ที่มีประสิทธิภาพมากขึ้นได้ นี่เป็นเทคโนโลยีดั้งเดิมของ Octra ในการใช้งาน FHE และทีมงานมีความสามารถด้านวิศวกรรมและการเข้ารหัสที่แข็งแกร่งมาก
Octra สร้างภาษาสัญญาอัจฉริยะใหม่ที่พัฒนาโดยใช้ไลบรารีโค้ด เช่น OCaml, AST, ReasonML (ภาษาที่ออกแบบมาโดยเฉพาะสำหรับสัญญาอัจฉริยะและแอปพลิเคชันที่โต้ตอบกับเครือข่ายบล็อกเชน Octra) และ C++ ไลบรารี Hyperghraph FHE ที่สร้างขึ้นสามารถใช้งานร่วมกับโปรเจ็กต์ใดก็ได้
สถาปัตยกรรมของมันยังคล้ายกับโปรเจ็กต์ต่างๆ เช่น Mind Network, Bittensor และ Allora โดยจะสร้างเครือข่ายหลัก จากนั้นโปรเจ็กต์อื่นๆ จะกลายเป็นซับเน็ตเพื่อสร้างสภาพแวดล้อมการทำงานที่แยกออกจากกัน ในเวลาเดียวกัน เช่นเดียวกับโปรเจ็กต์เหล่านี้ พวกเขาได้สร้างโปรโตคอลฉันทามติที่เกิดขึ้นใหม่ซึ่งเหมาะสมกับสถาปัตยกรรมมากกว่า .
หลักการทางเทคนิคของฉันทามตินี้ยังไม่ได้รับการเปิดเผย แต่เราสามารถคาดเดาได้คร่าวๆ อาจเป็นไปได้ว่ามีการส่งธุรกรรมไปยังเครือข่าย จากนั้นอัลกอริทึม SVM (Support Vector Machine) จะถูกนำมาใช้เพื่อกำหนดโหนดการประมวลผลที่ดีที่สุด โดยส่วนใหญ่จะขึ้นอยู่กับโหลดเครือข่ายปัจจุบันของแต่ละโหนด ระบบจะกำหนดเส้นทางฉันทามติโหนดพาเรนต์ที่ดีที่สุดตามข้อมูลประวัติ (การเรียนรู้อัลกอริทึม ML) ตราบใดที่ 1/2 ของโหนดมีความพึงพอใจ ก็สามารถเข้าถึงฉันทามติเกี่ยวกับฐานข้อมูลที่กำลังเติบโตได้
คาดหวัง
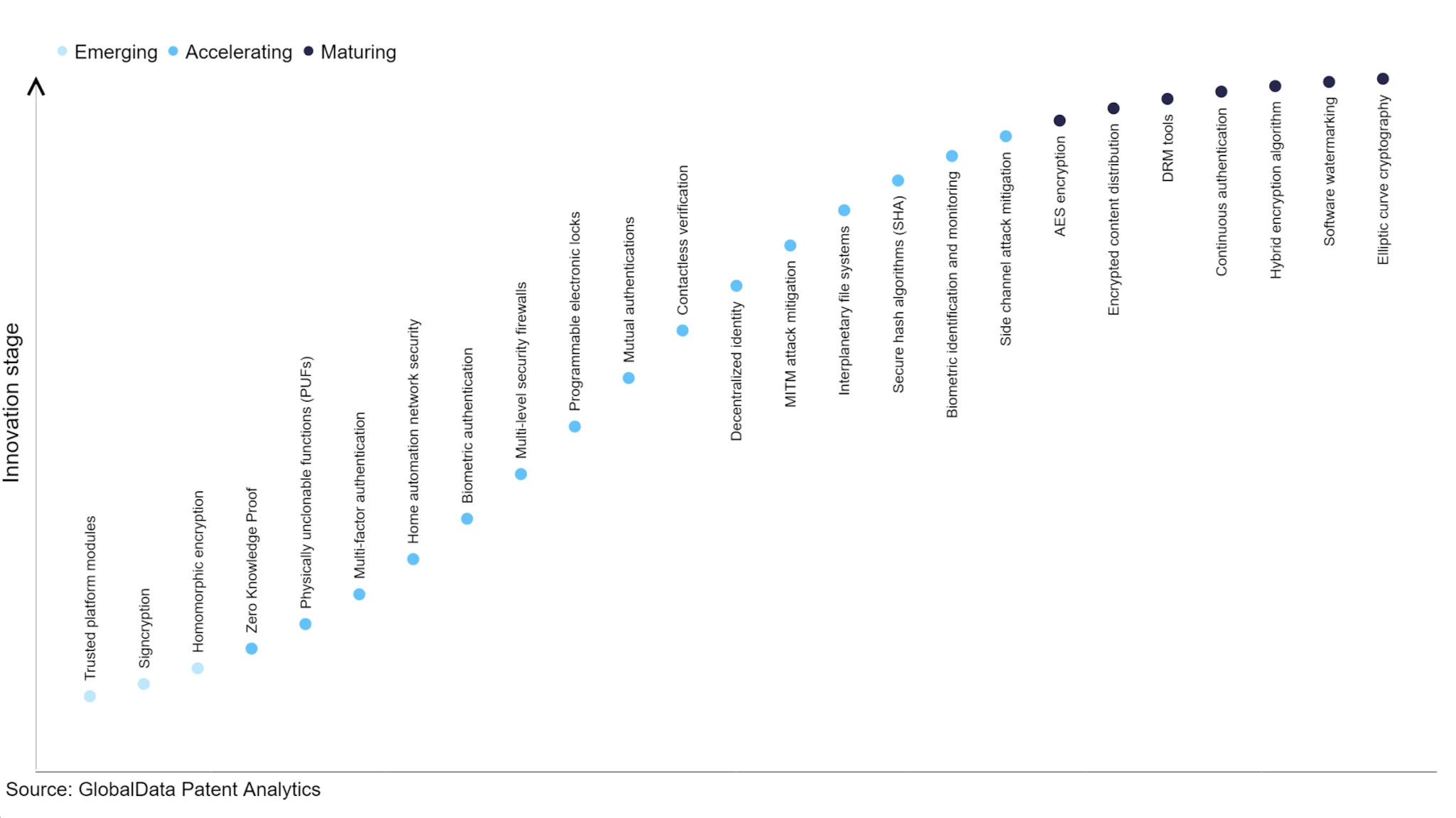
สถานะการพัฒนาเทคโนโลยีการเข้ารหัสที่ล้ำสมัย ที่มา: Verdict
เทคโนโลยี FHE เป็นเทคโนโลยีที่มุ่งเน้นอนาคต สถานะการพัฒนายังคงด้อยกว่าเทคโนโลยี ZK และขาดการลงทุน เนื่องจากมีประสิทธิภาพต่ำและต้นทุนสูงที่เกิดจากการปกป้องความเป็นส่วนตัว องค์กรเชิงพาณิชย์ส่วนใหญ่จึงไม่มีแรงจูงใจเพียงพอ การพัฒนาเทคโนโลยี ZK เร็วขึ้นเนื่องจากการลงทุนของ Crypto VC FHE ยังอยู่ในช่วงเริ่มต้น และถึงขณะนี้ ยังมีโครงการเพียงไม่กี่โครงการในตลาด เนื่องจากมีต้นทุนสูง ความยากด้านวิศวกรรมสูง และแนวโน้มที่ไม่ชัดเจนในเชิงพาณิชย์ ในปี 2021 DAPRA ร่วมมือกับบริษัทหลายแห่ง เช่น Intel และ Microsoft เพื่อเปิดตัวแผนการโจมตี FHE ระยะเวลา 42 เดือน แม้ว่าจะมีความคืบหน้าไปบ้าง แต่ก็ยังห่างไกลจากเป้าหมายด้านประสิทธิภาพที่บรรลุผล เนื่องจาก Crypto VC ให้ความสำคัญกับทิศทางนี้ เงินทุนจะหลั่งไหลเข้าสู่อุตสาหกรรมนี้มากขึ้น คาดว่าโครงการ FHE จะปรากฏในอุตสาหกรรมมากขึ้น และจะมีโครงการที่มีความสามารถด้านวิศวกรรมและการวิจัยที่แข็งแกร่งมากขึ้น เช่น Zama และ Octra A ทีมงานที่มีความสามารถยืนอยู่ตรงกลางเวที การผสมผสานระหว่างเทคโนโลยี FHE กับสถานะเชิงพาณิชย์และการพัฒนาของบล็อกเชนยังคงคุ้มค่าแก่การสำรวจ ในปัจจุบัน แอปพลิเคชันที่ดีที่สุดคือการไม่เปิดเผยชื่อของการโหวตโหนดการยืนยัน แต่ขอบเขตของแอปพลิเคชันยังคงแคบ
เช่นเดียวกับ ZK การใช้ชิป FHE เป็นหนึ่งในข้อกำหนดเบื้องต้นสำหรับการจำหน่าย FHE เชิงพาณิชย์ ในปัจจุบัน ผู้ผลิตหลายราย เช่น Intel, Chain Reaction, Optalysys ฯลฯ กำลังสำรวจแง่มุมนี้ แม้ว่า FHE เผชิญกับการต่อต้านทางเทคนิคมากมาย แต่ด้วยการใช้ชิป FHE การเข้ารหัสแบบโฮโมมอร์ฟิกอย่างสมบูรณ์ในฐานะเทคโนโลยีที่มีคำมั่นสัญญาที่ดีและความต้องการที่แน่นอน จะนำการเปลี่ยนแปลงอย่างลึกซึ้งมาสู่อุตสาหกรรม เช่น การป้องกันประเทศ การเงิน และการดูแลรักษาทางการแพทย์ โดยปล่อยศักยภาพของ การรวมข้อมูลส่วนตัวเหล่านี้เข้ากับเทคโนโลยี เช่น อัลกอริธึมควอนตัมในอนาคต จะนำไปสู่ช่วงเวลาที่ระเบิดได้
เรายินดีที่จะสำรวจเทคโนโลยีล้ำหน้าในยุคแรกเริ่มนี้ หากคุณกำลังสร้างผลิตภัณฑ์ FHE ที่สามารถนำไปใช้ในเชิงพาณิชย์ได้ หรือมีนวัตกรรมทางเทคโนโลยีที่ล้ำสมัยกว่านี้ โปรดติดต่อเรา!










